Optimal Monetary Policy According to HANK

This paper presents preliminary findings and is being distributed to economists

and other interested readers solely to stimulate discussion and elicit comments.

The views expressed in this paper are those of the authors and do not necessarily

reflect the position of the Federal Reserve Bank of New York or the Federal

Reserve System. Any errors or omissions are the responsibility of the authors.

Federal Reserve Bank of New York

Staff Reports

Optimal Monetary Policy

According to HANK

Sushant Acharya

Edouard Challe

Keshav Dogra

Staff Report No. 916

February 2020

Optimal Monetary Policy According to HANK

Sushant Acharya, Edouard Challe, and Keshav Dogra

Federal Reserve Bank of New York Staff Reports, no. 916

February 2020

JEL classification: E21, E30, E52, E62, E63

Abstract

We study optimal monetary policy in a heterogeneous agent new Keynesian economy. A

utilitarian

planner seeks to reduce consumption inequality, in addition to stabilizing output gaps

and inflation. The

planner does so both by reducing income risk faced by households, and by

reducing the pass-through from

income to consumption risk, trading off the benefits of lower

inequality against productive inefficiency

and higher inflation. When income risk is

countercyclical, policy curtails the fall in output in recessions

to mitigate the increase in

inequality. We uncover a new form of time inconsistency of the Ramsey plan—the temptation to

exploit households' unhedged interest rate exposure to lower inequality.

Key words: new Keynesian model, incomplete markets, optimal monetary policy

_________________

Acharya, Dogra: Federal Reserve Bank of New York (emails: sushant.acharya@ny.frb.org,

keshav.dogra@ny.frb.org). Challe: CREST and Ecole Polytechnique (email:

edouard.chal[email protected]). The authors thank Florin Bilbiie, Christopher Carroll, Russell

Cooper, Clodomiro Ferreira, Antoine Lepetit, Galo Nuño, Pedro Teles, Gianluca Violante, and

Pierre-Olivier Weil for helpful discussions. They also received useful comments from seminar

participants at HEC Paris, UT Austin, UC3M, EUI, Université Paris-Dauphine, Université Paris

8, Banque de France, and CREST, as well as from conference participants at the Barcelona GSE

Summer Forum (Monetary Policy and Central Banking), the NBER Summer Institute (Micro

Data and Macro Models), the Salento Macro Meetings, SED, and T2M. Edouard Challe

acknowledges financial support from the French National Research Agency (Labex

Ecodec/ANR-11-LABX-0047). The views expressed in this paper are those of the authors and do

not necessarily reflect the position of the Federal Reserve Bank of New York or the Federal

Reserve System.

To view the authors’ disclosure statements, visit

https://www.newyorkfed.org/research/staff_reports/sr916.html.

1 Introduction

It is increasingly recognized by researchers and policymakers that monetary policy can have important

eﬀects on inequality. Despite this, the study of how monetary policy should be conducted optimally has

only recently begun to depart from a representative agent framework in which concerns about inequality

are trivially absent. While the large recent heterogeneous agent New Keynesian (HANK) literature has

shown that uninsurable idiosyncratic risk and inequality can dramatically change the positive eﬀects of

monetary policy on the macroeconomy (See for example Ravn and Sterk (2017, Forthcoming); Kaplan et

al. (2018); den Haan et al. (2018); Auclert et al. (2018); Auclert (2019); Bilbiie (2019a) and many others),

the normative implications of HANK and the reciprocal eﬀects of monetary policy on risk and inequality,

have been less well studied. This gap in the literature partly exists because characterizing optimal policy

in HANK economies is technically diﬃcult. Solving for the Ramsey optimal policy involves choosing the

evolution of an inﬁnite dimensional state variable (the wealth distribution), as well as inﬁnite dimensional

controls (the distribution of consumption and hours worked across agents) subject to an inﬁnite number

of constraints (each household’s optimality condition and budget constraints).

One approach to solving optimal policy problems for HANK economies is computational, and re-

searchers have recently started developing numerical algorithms to handle them (Bhandari et al., 2018).

We instead take an analytical approach. We study a standard NK economy with nominal rigidities with

the exception that households face uninsurable idiosyncratic risk. Markets are incomplete and agents can

only self-insure by trading a riskless bond or by working longer hours. We assume that households have

constant absolute risk (CARA) utility and idiosyncratic shocks are normally distributed. As in Acharya

and Dogra (2018), these assumptions imply that the economy permits linear aggregation which in turn

means that the inﬁnite dimensional distributions of consumption, hours worked and wealth can be summa-

rized by their cross-sectional averages: the positive behavior of macroeconomic aggregates can be described

independently of the distribution of the wealth distribution. Of course, from a normative perspective, the

dispersion of wealth does aﬀect social welfare and hence the optimal conduct of monetary policy. Crucially,

the eﬀect of inequality on social welfare is also summarized by a ﬁnite dimensional suﬃcient statistic. This

makes the optimal policy problem analytically tractable, allowing us to drill down and identify exactly the

features that makes the optimal conduct of monetary policy diﬀerent in HANK economies compared to

the RANK benchmark.

As is commonly known, in RANK the planner seeks to stabilize prices and keep output at its produc-

tively eﬃcient level. In HANK, the planner has an additional objective - to use monetary policy to reduce

the cross-sectional consumption dispersion that results from the cumulated eﬀects of uninsured idiosyn-

cratic shocks. This incentive is shut down in RANK by construction. We show that there are three ways in

which the planner can use monetary policy to achieve this purpose. First, the central bank may attempt

to reduce the amount of income risk that households are exposed to (the income risk channel). How to

achieve this reduction naturally depends on the cyclicality of income risk: if this risk is countercyclical,

then the central bank has an incentive to raise output in order to lower risk, while the opposite is true

if risk is procyclical. Either way, the central bank’s willingness and ability to manipulate the amount of

idiosyncratic risk that households face gives it an incentive to move output away from the level consistent

with stable prices and productive eﬃciency.

The second way in which the central bank may reduce consumption dispersion, independently of aﬀect-

ing the level of income risk, is by reducing the pass-through from income risk to consumption risk, that is,

by lowering the marginal propensity to consume out of a change in individual income (the self-insurance

channel). This pass-through ultimately reﬂects the ability of the households to self-insure against idiosyn-

cratic risk through borrowing or working longer hours, and is thus aﬀected by the paths of real interest

rates and wages going forward. On the one hand, lower interest rates make it easier for households to

borrow in response to an unfavorable shock, making individual consumption less response to changes in

individual income; this ultimately reduces consumption dispersion at any level of income risk. On the other

hand, higher wages going forward make it easier for households to buﬀer the impact of a fall in current

income on current consumption by borrowing today and working longer hours in the future to repay the

debt. When future wages are high, only a small increase in hours ( and hence the incurred dis-utility)

worked is required to repay this debt. This again makes individual consumption less responsive to changes

in current income. It follows that the central bank has an incentive to commit to low interest rates and

high wages –i.e., to be expansionary– going forward in order to reduce the pass-through from income risk

to consumption risk. This incentive is of course absent in RANK.

Finally, the central bank can reduce consumption dispersion through unanticipated changes in the

marginal propensity to consume out of wealth. Given a distribution of wealth, an unexpected fall in

interest rates beneﬁts poor debtors, reducing their interest payments and increasing their consumption

(the unhedged interest rate exposure (URE) channel) (Auclert, 2019). Conversely, lower interest rates

reduce the interest income of rich savers, reducing their consumption. Overall, lower rates reduce the

marginal propensity to consume out of wealth, reducing consumption inequality. Importantly, this channel

(unlike the previous two) only operates for unexpected changes in interest rates, as we explain in more

detail in Section 4.

How does the presence of these three channels, through which the planner can aﬀect inequality, change

the optimal conduct of monetary policy? As is commonly known, in RANK, optimal monetary policy

features divine coincidence in response to productivity shocks (Blanchard and Gal´ı, 2007): it is both

feasible and optimal to stabilize both the gap between output and its eﬃcient level (output gap), and

inﬂation. In our RANK economy, in the empirically relevant case where income risk is countercyclical,

while it remains feasible to stabilize the output gap and inﬂation, it is no longer optimal to do so. But

to understand the tradeoﬀs that lead the planner to deviate from divine coincidence in this case, it is

instructive to start by examining a HANK economy where divine coincidence is optimal. This is the case

when risk is mildly procyclical and there is no initial wealth inequality. In this knife-edge case, the two

channels through which anticipated monetary policy aﬀects consumption inequality exactly oﬀset each

other: expansionary policy raises output and hence income risk, but makes it easier for households to self-

insure, leaving the consumption risk faced by households unchanged. In addition, the absence of wealth

inequality at date 0 mutes the URE channel. Thus, while the planner would like to reduce consumption

inequality, since it is not possible to do this with monetary policy, it remains optimal to stabilize both the

Earlier work has stressed that the cyclicality of income risk aﬀects the response of aggregate demand in HANK economies

(Werning, 2015; Acharya and Dogra, 2018; Bilbiie, 2019a), and this in itself generically requires a benevolent central bank

to implement a diﬀerent path of the policy rate than in RANK (Challe, 2020). This does not, however, necessarily warrant

departing from price stability.

output gap and inﬂation.

Away from this knife-edge case, monetary policy can, and does exploit the channels above to aﬀect

consumption inequality. Suppose ﬁrst that risk remains mildly procyclical so that income risk and self-

insurance channels oﬀset each other, but there is wealth inequality at date 0. In this case, monetary policy

cannot aﬀect inequality through the ﬁrst two channels, but it can through the URE channel. Consequently,

the optimal plan features an unexpected cut in interest rates at date 0, which reduces consumption in-

equality at the cost of deviating from the eﬃcient level of output and inﬂation. That is, optimal policy

features higher output and inﬂation at date 0 than would be optimal in RANK. While monetary policy

cannot aﬀect inequality from date 1 onwards, output and inﬂation continue to deviate from RANK as

policy seeks to smooth the transition back to steady state. If policy was somehow prevented from creating

the boom to exploit the URE channel at date 0, it would not seek to deviate from RANK at any other

date either.

This brings us to the empirically relevant case of countercyclical risk. In this case expansionary mone-

tary policy can reduce inequality at all dates through the self-insurance and income risk channels: a lower

path of interest rates makes it easier for households to insure themselves, and makes a boom in output

which reduces the level of income risk households face. In addition, at date 0, a cut in rates delivers a

further reduction in inequality through the URE channel. Consequently, the planner always trades oﬀ this

beneﬁt of more expansionary monetary policy - namely, that it reduces consumption inequality - against

the costs of ineﬃciently high output and inﬂation. These tradeoﬀs change the optimal response to produc-

tivity shocks, relative to RANK. Following a negative productivity shock, the planner lets output decline

as much as output in the ﬂexible price case and implements zero inﬂation by raising nominal interest rates.

However, in HANK, optimal policy implements a lower path of nominal interest rates, curtailing the fall

in output in order to mitigate the increase in inequality. Even though this entails higher inﬂation and

output above its eﬃcient level, this is optimal because inequality is already higher in recessions and so is

the beneﬁt from a reduction in inequality.

So far we have only discussed one channel through which unexpected cuts in interest rates can lower

inequality (the URE channel). Several authors have highlighted another way in which unexpected changes

in monetary policy can lower inequality, namely the Fisher channel: unexpected inﬂation redistributes

from savers who hold nominal assets to debtors who hold nominal liabilities. We deliberately abstract

from this channel in our baseline model (by letting households trade inﬂation-indexed debt) in order to

emphasize that the URE channel does not depend on the ability of monetary policy to redistribute wealth

through an inﬂation surprise. While conceptually distinct from the URE channel, the Fisher channel

provides another avenue through which expansionary monetary policy can reduce inequality. In Section

6 we show that when households trade nominally denominated assets, optimal monetary policy is more

expansionary in recessions compared to RANK.

Related Literature The paper most closely related to ours is Bhandari et al. (2018), who also study

optimal monetary policy in a HANK model. The main diﬀerence between our paper and theirs is method-

ological. Bhandari et al. (2018) propose a numerical algorithm to derive optimal monetary policy in HANK

models, while we study a HANK economy with constant constant absolute risk aversion (CARA) prefer-

ences and normally distributed shocks which permits closed form solutions.

We see the two approaches as

inherently complementary: the ﬁrst allows more ﬂexibility in the structure of preferences and idiosyncratic

shocks, while the second better isolates the channels by which the central bank manipulates consumption

dispersion along the optimal policy plan. Another closely related paper is Nu˜no and Thomas (2019) who

study how URE and Fisher eﬀects aﬀect the optimal conduct of monetary policy in the presence of het-

erogeneity. Unlike us, they study a small open economy in which short-term real interest rates and output

are unaﬀected by monetary policy. Thus, the classic output inﬂation trade-oﬀ which is central to New

Keynesian economies is absent in their setting.

Several authors have studied optimal monetary policy in simple HANK economies with limited cross-

sectional heterogeneity–see, e.g., Bilbiie (2008); Bilbiie and Ragot (2018); Bilbiie (2019a) and Challe

(2020).

Most of these papers achieve tractability by imposing the zero liquidity limit (households can-

not borrow and government debt is in zero net supply).

This assumption rules out the self-insurance

channel because in equilibrium households do not borrow or lend and hence they spend all their income

on consumption. Our analysis shows that this assumption rules out an important channel through which

monetary policy aﬀects inequality.

More generally, our paper belongs to the growing strand of literature that revisits the transmission and

optimality of various economic policies within the HANK framework. This includes not only the work on

conventional monetary policy discussed above but also that on unconventional monetary policy (McKay

et al., 2016; Acharya and Dogra, 2018; Bilbiie, 2019a; Cui and Sterk, 2019), on unemployment-insurance

and social-insurance policies (McKay and Reis, 2016, 2019; den Haan et al., 2018; Kekre, 2019), and on

ﬁscal policy (Auclert et al., 2018; Bilbiie, 2019b).

The rest of the paper is organized as follows. Section 2 presents the model. Section 3 characterizes

equilibria, deﬁning the implementability constraints the planner faces. Section 4 shows that the utilitarian

planner’s objective function can be written in terms of aggregate variables and a single suﬃcient statistic

for the welfare-relevant measure of inequality. Section 5 characterizes optimal monetary policy. Section 6

introduces nominal bonds and shows how our results extend to that case. Section 7 concludes.

2 Environment

2.1 Households

We study a Bewley-Huggett economy in which households face uninsurable idiosyncratic shocks to their dis-

utility from supplying labor. We abstract from aggregate risk but allow for a one time unanticipated shock

at date 0, after which agents have perfect foresight. Our economy features a perpetual youth structure `a la

Blanchard-Yaari in which each individual faces a constant survival probability ϑ in any period. Population

is ﬁxed and normalized to 1. Consequently, the size of a newly born cohort at any date t is 1 − ϑ and the

Caballero (1990), Calvet (2001), Wang (2003), Angeletos and Calvet (2006) have used similar modeling assumptions in

real economies. Recently, Acharya and Dogra (2018) shows that these assumptions are very helpful in understanding the

positive properties of HANK economies.

See also Nistic`o (2016), who generalizes the Two-Agent New Keynesian (TANK) model of Gal´ı et al. (2007) and Bilbiie

(2008) to the case of stochastic asset-market participation, and Debortoli and Gal´ı (2018) on the comparison between the

TANK model and a HANK model with homogeneous borrowing-constrained households and heterogeneous unconstrained

households.

Bilbiie and Ragot (2018) is an exception as it it allows agents to hold money in positive amounts for self-insurance purposes.

date t size of a cohort born at s < t is (1 −ϑ)ϑ

t−s

. The date s problem of an individual i born at date s is:

max

(i),`

(i),a

(i)}

∞

t=s

(βϑ)

t−s



(i), `

(i); ξ

(i)



s.t.

(i) + q

t+1

(i) = w

(i) + a

(i) + T

(1)

(i) = 0 (2)

Agents have CARA preferences over both consumption and (disutility of) labor:



(i), `

(i); ξ

(i)



= −

−γc

(i)

− ρe

(i)−ξ

(i)]

(3)

Each agent i saves in riskless real actuarial bonds, issued by ﬁnancial intermediaries (described below),

which trade at a price of q

at date t and pay oﬀ one unit of the consumption good at t + 1 if the agent

survives.

Each agent can take unrestricted positive or negative positions in the bond and these choices are

only disciplined by the transversality condition. T

denotes lump-sum transfers net of taxes and dividends

from the ﬁrms. For simplicity, we assume that dividends are equally distributed across agents.

A household supplies labor `

(i) at the pre-tax real wage w

. The agent faces uninsurable shocks ξ

(i) ∼



ξ, σ



to the dis-utility of supplying labor. ξ

(i) is independent across time and across individuals. A

larger realization of ξ

(i) reduces the dis-utility from work and, given wages, increases the household’s labor

supply. Equivalently, one may think of ξ

(i) as a shock to the household’s endowment of time available to

supply labor.

To see this, deﬁne leisure as l

(i) = ξ

(i) − `

(i). Then one can rewrite the period utility

functional (3) as −e

−γc

(i)

/γ − ρe

−l

(i)/ρ

and the budget constraint as:

(i) + w

(i) + q

t+1

(i) = w

(i) + a

(i) + T

(4)

The LHS of (4) denotes the purchases of consumption, leisure and bonds by the household while the RHS

denotes the notional cash-on-hand - the value of the household’s time endowment along with savings net

of transfers. Henceforth, we will simply refer to this as cash-on-hand. We allow for the possibility that the

variance of ξ, σ

, vary endogenously with the level of economic activity as we discuss below.

2.2 Financial intermediaries

There is a competitive ﬁnancial intermediation sector which trades actuarial bonds with households and

trades government debt. An intermediary only needs to repay households that survive between t and t + 1.

In economies with a distribution of nominal debt, unexpected inﬂation redistributes wealth between creditors and debtors.

Bhandari et al. (2018) and Nu˜no and Thomas (2019) discuss how optimal monetary policy takes this into account. Our

benchmark economy deliberately abstracts from this channel in order to highlight the other ways in which optimal monetary

policy diﬀers in HANK and RANK economies. In Section 6, we replace real debt with nominal debt, bring this channel back

into play and show how our results change.

We thank Gianluca Violante for suggesting this interpretation.

The representative intermediary solves:

max

t+1

−ϑa

t+1

+ B

t+1

s.t. −q

t+1

+ Π

t+1

1 + i

≤ 0

where B

denotes government debt, a

denotes claims held by households, R

1+i

t+1

is the gross real

return on government debt, i

is the nominal interest rate which is set by the monetary authority and Π

t+1

denotes gross inﬂation between t and t +1. Zero proﬁts require that the intermediary sells/buy bonds from

the households at a price q

and that ϑa

t+1

= B

t+1

2.3 Final goods producers

A representative competitive ﬁnal goods ﬁrm transforms the diﬀerentiated intermediate goods y

, j ∈ [0, 1]

into the ﬁnal good y according to the CES aggregator y

(j)

. As is standard, the ﬁnal good

producer’s demand for variety j is:

(j) =



(j)



−

λ−1

(5)

where

λ−1

is the elasticity of substitution between varieties.

2.4 Intermediate goods producers

There is a continuum of monopolistically competitive intermediate goods ﬁrms indexed by j ∈ [0, 1]. Each

ﬁrm faces a quadratic cost of changing the price of the variety it produces (Rotemberg, 1982). If ﬁrm j

hires n

(j) units of labor, it can only sell to the ﬁnal goods ﬁrm the quantity:

(j) = z

(j) −



(j)

t−1

(j)

− 1



(6)

where z

denotes the level of aggregate productivity at date t. Firm j solves:

max

}

∞

t=0

∞

t=0

t|0



(j)

(j) − (1 − τ)w

(j)



subject to (5) and (6) where Q

t|0

s=0

−1

. This yields the standard Phillips curve:

(Π

− 1) Π

Φ (λ − 1)



1 −

(1 − τ) λw





t+1



(Π

t+1

− 1) Π

t+1

(7)

2.5 Government

The monetary authority sets the interest rate on nominal government debt. The ﬁscal authority subsidizes

the wage bill of ﬁrms at a rate τ and rebates lumpsum taxes/transfers to all households equally. The

government budget constraint is given by:

t+1

1 + i

= P

+ τP

(j)dj + B

(8)

We further assume that government debt is in zero net supply, B

= 0 for all t ≥ 0.

2.6 Market clearing

In equilibrium, the markets for the ﬁnal good, labor and assets must clear:

= (1 − ϑ)

s=−∞

s−t

(i)di

(j)dj = (1 − ϑ)

s=−∞

s−t

(i)di

0 = a

= (1 − ϑ)

s=−∞

s−t

t+1

(i)di

where the last equation holds because B

= 0 for all t.

2.7 Shocks

As mentioned previously, we abstract from aggregate risk but allow for a one time unanticipated aggregate

shock to the level of labor productivity z

at date 0. We assume that the shock decays geometrically:

ln z

= %

ln z

for %

∈ [0, 1).

3 Characterizing equilibria

As in Acharya and Dogra (2018), CARA preferences and normally distributed shocks imply that the

model aggregates linearly and the distribution of wealth does not directly aﬀect the dynamics of aggregate

variables. We begin by describing optimal household decisions in equilibrium.

Proposition 1 (Household Decision Rules). In equilibrium, the optimal date t consumption and labor

supply decisions of a household i born at date s are:

(i) = C

+ µ

(i) (9)

(i) = ρ ln w

− γρc

(i) + ξ

(i) (10)

where x

(i) = a

(i) + w



(i) −



is demeaned cash-on-hand, C

denotes aggregate consumption and µ

is the “marginal propensity to consume” (MPC) out of cash-on-hand. These evolve according to:

= −

ln βR

+ C

t+1

−

γµ

t+1

(11)

−1

= 1 + γρw

−1

t+1

(12)

Proof. See Appendix A

To understand the role of market incompleteness in explaining the behavior of consumption and la-

bor supply it is useful to compare equations (9) and (10) to their counterparts under complete markets.

Under complete markets, all households are insured against dis-utility shocks, i.e. the marginal utility of

consumption e

−γc

(i)

and the marginal dis-utility of work e

(i)−ξ

(i))

are equalized across all states and

so:

∂c

(i)

∂ξ

(i)

= 0 and

∂`

(i)

∂ξ

(i)

= 1. Thus, since households’ consumption is insured, a household which draws a

temporarily higher dis-utility from working can reduce hours without experiencing a drop in consumption.

Instead, when markets are incomplete (9) and (10) imply that:

∂c

(i)

∂ξ

(i)

= µ

> 0 and

∂`

(i)

∂ξ

(i)

= 1 − γρµ

< 1

For example, after a negative ξ shock (i.e., greater dis-utility from working), consumption declines instead

of remaining constant while labor supply does not fall quite as much as under complete markets. While

households use credit and labor market to insure themselves to some extent, these are not perfect substitutes

for Arrow securities, so agents are only able to partially insulate themselves from the shock. When the

dis-utility of labor rises, households would like to work less, but reducing hours as much as under complete

markets would cause consumption to drop too much. The optimal response to the shock is to use labor

supply for self-insurance, i.e. to work longer hours than under complete markets.

Proposition 1 also states that the MPC out of cash-on-hand is the same across individuals; (12) describes

its evolution over time. Intuitively, consider a household i that receives an additional dollar at date t. They

will optimally choose to spend dc

(i) = µ

of the dollar in the current period. Since consumption and leisure

are normal goods, they also reduce hours worked by γρµ

, resulting in γρw

less income. Saving the

remaining 1 − µ

(1 + γρw

), they ﬁnd themselves with da

t+1

(i) =

[1 − µ

(1 + γρw

)] next period out

of which they will consume dc

t+1

(i) = µ

t+1

(i). Finally, it is optimal to smooth consumption so that

(i) = dc

t+1

(i) which yields µ

= µ

t+1

[1 − µ

(1 + γρw

)]. Rearranging this expression yields equation

(12). Iterating forwards yields:

∞

s=0

t+s|t

(1 + γρw

t+s

)

The MPC µ

, which measures the pass-through from a fall in cash-on-hand to consumption, is increasing in

current and future interest rates and decreasing in current and future wages. This is because interest rates

and wages aﬀect households’ ability to use the bond and labor markets, respectively, for self-insurance.

Consider a household who receives an unfavorable shock ξ < 0. The household responds by working less

today, borrowing in order to mitigate the decline in consumption, and working longer hours in the future.

A lower path of interest rates reduces the cost of borrowing, making it easy to self insure using the bond

market and lowering the responsiveness of consumption to changes in cash-on-hand. Similarly, higher

future wages reduce the (disutility) cost of working more hours in the future since even a small increase

in hours worked suﬃces to repay the same debt. This too lowers the sensitivity µ

of consumption to

cash-on-hand.

While the sensitivity of household consumption to shocks (µ

) depends on the factors we have just

described, the average level of consumption in the economy C

depends on interest rates relative to impa-

As already mentioned, the model can be re-interpreted as one with an idiosyncratic time-endowment shock and utility

from leisure time. In this interpretation, both consumption and leisure time stay constant under complete markets, while both

co-vary with the idiosyncratic shock under incomplete markets.

While Acharya and Dogra (2018) already discuss how the MPC responds to future real interest rates, the path of wages

has no eﬀect on the MPC in their paper because their environment features inelastic labor supply. In this model, however,

since households can choose how much labor to supply, they use this additional margin to self-insure.

tience and households’ desire for precautionary savings, as shown in equation (11). Absent idiosyncratic

risk, σ

= 0, (11) is a standard Euler Equation; higher real interest rates relative to household impatience

raise consumption growth. The last term in (11) reﬂects precautionary savings. Given (9), the conditional

variance of date t + 1 consumption of household i is V



t+1

(i)



= µ

t+1

. To the extent that

consumption risk is positive and households are prudent (γ > 0), households save more than in a riskless

economy for the same interest rate, i.e. they choose a steeper path of consumption growth. The variance

of consumption, in turn, depends on both the variance of cash-on-hand V



t+1

(i)



= w

t+1

, and the

pass-through of cash-on-hand risk into consumption risk measured by the (squared) MPC µ

t+1

Determination of y

In a symmetric equilibrium, aggregating (6) across ﬁrms, we have:

= z

−

(Π

− 1)

(13)

Aggregating labor supply (10) across currently alive households and using goods and labor market clearing:

= ρ ln w

− γρy

+ ξ (14)

Combining the two equations above, we have:

= z

ρ ln w

+ ξ

1 + γρz

(Π

− 1)

(15)

where

(Π

− 1)

denotes the resource cost of inﬂation - higher inﬂation reduces output.

Deriving the aggregate IS equation Imposing goods market clearing in (11) yields the aggregate IS

equation which describes the relation between output today and tomorrow:

= y

t+1

−

ln β



i + i

t+1



−

γµ

t+1

(16)

Time varying σ

Following McKay and Reis (2019), we allow for the variance of ξ shocks to vary

endogenously with economic activity so that the model generates cyclical changes in the distribution of

earnings risks. In particular, we assume that σ

= σ

2φ(y

−y)

where y denotes steady state output

and φ =

∂ ln V(x)

∂y

is the constant semi-elasticity of the variance of cash-on-hand w.r.t output. This ﬂexible

speciﬁcation allows the variance of cash-on-hand V

(x) to be either increasing in y

(procyclical risk), when

φ > 0; decreasing in y

(countercyclical risk), when φ < 0; or independent of the level of y

(acyclical risk)

when φ = 0.

3.1 Steady state

We now characterize allocations in the zero inﬂation steady state. We normalize the level of productivity

z = 1 in steady state. Imposing Π

= Π

t+1

= 1 in (7) requires that steady state wages w =

λ(1−τ)

. Given

this wage, steady state output is y =

ρ ln w+ξ

1+γρ

. Imposing steady state in (16) and (12) yields:

R = β

−1

−

and µ =

1 −

1 + γρw

(17)

where Λ = γ

denotes the consumption risk faced by households in steady state (scaled by the

coeﬃcient of prudence) and

β =

is the steady state price of an actuarial bond. Observe that the

presence of uninsurable risk (Λ > 0) implies that the equilibrium real interest rate R < β

−1

. Furthermore,

the steady state distribution of cash-on-hand x in the population is given by:

F (x) = (1 − ϑ)

∞

s=0



wσ

√

s + 1



(18)

where Φ(·) is the cdf of the standard normal distribution. This follows since, conditional on survival, x is

a random walk with no drift and a variance of w

in steady state.

3.2 Linearized demand block

The demand block of the economy, given a path of interest rates, can be described by the IS equation

(16), the MPC recursion (12) and the deﬁnition of GDP (15). Before analyzing optimal policy, it is useful

to compare the dynamics of this HANK economy to its RANK counterpart. It is easiest to compare the

ﬁrst-order Taylor expansion of the equations describing aggregate dynamics in the neighborhood of the

zero inﬂation steady state, which are:

= Θby

t+1

−

− π

t+1

) −

Λbµ

t+1

(19)

bµ

= −(1 −

β)

γρw

1 + γρw

β (bµ

t+1

+ i

− π

t+1

) (20)

1 + γρ

(21)

where Θ = 1 −

Λφ

. In RANK, there is no idiosyncratic risk, i.e. σ

= 0 which implies Θ = 1 and Λ = 0, so

that (19) becomes the standard RANK IS curve. As discussed in Acharya and Dogra (2018), uninsurable

idiosyncratic risk changes the IS equation in two ways. First, it can introduce either discounting (Θ < 1)

or compounding (Θ > 1) depending on the cyclicality of risk. If risk is acyclical, φ = 0, then Θ = 1 as

in the RANK IS equation. If risk is procyclical φ > 0 then Θ < 1 and there is discounting in the IS

equation. This is because in this situation low future output implies low idiosyncratic income risk, hence

(all else equal) a fall in precautionary savings that mutes down the eﬀect of the forthcoming recession

on current aggregate demand. The opposite occurs when risk is countercyclical (φ < 0), in which case

Θ > 1 –that is, we have compounding in the IS equation–, because then the impact of a future recession

on current aggregate demand is magniﬁed by the rise in precautionary savings. Second, the strength of

the precautionary motive depends not only on the level of income risk but also on its pass-through to

consumption risk, i.e. bµ

t+1

, which in turn depends of the future path of real interest rates and wages. By

committing to a lower path of real rates or a higher path of wages, monetary policy can lower the strength

We linearize y

and w

in levels while all other variables are log-linearized.

of the precautionary savings motive at any level of income risk.

Equations (7), (12), (15) and (16) summarize the optimality conditions of the private sector and deﬁne

the implementability constraints faced by the central bank. We may now turn to its objective function.

4 Objective function of the planner

We assume that the planner maximizes a utilitarian criterion; at any date t the planner assigns equal

weights to the welfare of all households currently alive and a weight of β

s−t

on the welfare of cohorts

who will be born at dates s > t. Given these Pareto weights, the planner’s objective can be written as

maximizing

∞

t=0

where U

, the period t felicity function of the planner is simply the average utility

of all surviving agents:

= −(1 − ϑ)

s=−∞

−s



(i), `

(i); ξ

(i)



di,

This expression for U

feature the full cross-sectional distribution of agents and is in general not tractable.

Fortunately, it can be greatly simpliﬁed by exploiting our CARA-Normal structure again.

Proposition 2 (Social Welfare Function). The period felicity function U

can be written as

= u(y

, n

; ξ)Σ

where

= (1 − ϑ)

s=−∞

−s

(t,s)

and σ

(t, s) is the date-t cross-sectional dispersion of consumption amongst the surviving households from

the cohort born at date s ≤ t, i.e., c

(i) ∼ N



, σ

(t, s)



Proof. See Appendix B.2.

Intuitively, u(y

, n

; ξ) is the notional ﬂow utility of the representative agent, i.e., the period utility

functional (3) evaluated at aggregate consumption y

, aggregate labor supply n

, and mean labor dis-

utility ξ. Σ

can be thought of as the welfare cost of inequality, and is increasing in the within cohort

dispersion of consumption. In a riskless economy, there would be no consumption dispersion and hence

= 1 at all dates. However, in the presence of risk, Σ

> 1, reducing welfare relative to this representative

agent benchmark. Recall that u(·) < 0 and so higher Σ

reduces welfare.

Note that the planner discounts felicity at the same rate as the households would themselves. Consider a change in

allocations which reduces the date t felicity of cohort s by du

and increases their date t + 1 felicity by du

t+1

, while keeping

the felicity at all other dates and for all other agents the same. A cohort s individual will be indiﬀerent regarding this change

if du

= βϑdu

t+1

. From the planner’s perspective this changes aggregate welfare by −ϑ

s−t

+ βϑ

s+1−t

t+1

. Thus, the

planner will be indiﬀerent about this change if and only if the individuals themselves are indiﬀerent. As discussed by Calvo

and Obstfeld (1988), assuming that the planner and the households share the same rate of time preference ensures that social

preferences are time-consistent, so that the ﬁrst-best intertemporal allocation of consumption across cohorts does not change

over time. This does not prevent other from of time inconsistencies from arising in decentralized equilibrium (as shown below),

but these are unrelated to the form of social preferences.

Appendix B.2.1 shows that the evolution of Σ

for t > 0 can be written as:

ln Σ

+ ln [1 − ϑ + ϑΣ

t−1

] (22)

with

ln Σ

+ ln [1 − ϑ + ϑΣ

−1

] + ln





1 − ϑe



−1







| {z }

eﬀect of date 0 surprise / URE

(23)

where Σ

−1

= Σ =

(1−ϑ)e

1−ϑe

is the steady state Σ.

Intuitively, higher cash-on-hand risk w

and a higher

pass-through µ

both tend to increase consumption inequality. In addition, consumption inequality inherits

the slow moving dynamics of wealth inequality, as can be seen from the presence of Σ

t−1

in (22).

Equation (23) shows that the relation between µ

and Σ

is diﬀerent than the relation between µ

and Σ

at all other dates. This can be explained intuitively as follows. At the beginning of date 0, the

distribution of wealth a is at its steady state level: some households have positive net wealth and some

are debtors. Since savers and debtors have diﬀerent unhedged interest rate exposures (UREs) in the sense

of Auclert (2019), an unanticipated change in interest rates aﬀects consumption inequality. Suppose that

at date 0, the central bank chooses a policy path that implements a transitory drop in the real interest

rate. The lower interest rates beneﬁt poor debtors, reducing their interest payments and allowing them to

increase their consumption. By the same token, a lower path of rates reduces the interest income of rich

savers, causing them to reduce consumption. In other words, lower rates reduce the MPC out of wealth

(µ

↓) which reduces consumption inequality and hence Σ

Importantly, an anticipated cut in rates would not reduce inequality as much as this unanticipated cut.

If wealthy agents at date t − 1 anticipated lower rates at date 0, they would save more in order to insure

a higher level of consumption at date 0. Equally, the poor debtors would borrow more at date -1 knowing

that their debt would be less costly to repay. For this reason, what reduces Σ

through this channel is not

a fall in µ

per se but a fall in µ

relative to its expected value E

−1

, as can be seen from the last term

in (23). To be clear, anticipated cuts in rates do reduce inequality as discussed earlier: lower µ

reduces

in equation (22). But there is an additional eﬀect that comes from a surprise fall in rates. In our

environment, since we do not have aggregate shocks (except for the unanticipated shock at date 0) and the

fact that the Ramsey planner is only allowed to re-optimize at date 0 imply that this additional aﬀect of

an unanticipated change in µ can only occur at date 0. More generally, in an environment with aggregate

shocks, surprise changes in µ would have this eﬀect on any date, for example when there is an aggregate

productivity shock and z

6= E

t−1

Of course, this one-oﬀ redistribution would not operate in the absence of wealth inequalities at time

0. If the economy were starting with equal (zero) wealth for all households, instead of starting from the

invariant distribution, then only the ﬁrst eﬀect would play out and the equilibrium value of consumption

We are assuming that the economy is in steady state at date −1.

Note that within-cohort consumption dispersion σ

(t, s) in general rises without bounds as the cohort ages (i.e., as

t − s → ∞), due to the cumulated eﬀect of idiosyncratic shocks on the distribution of cash-on-hand. However, since every

cohort gradually shrinks in size, while newborn cohorts have little consumption dispersion (i.e., σ

(t, t) = µ

), Σ

does

not necessarily blow up. In fact, provided that the survival rate ϑ < e

−Λ/2

, Σ

is stationary.

dispersion at time zero would simply be:

ln Σ

. (24)

5 Optimal monetary policy

The planner chooses sequences {w

, Π

, µ

, Σ

, i

, n

}

∞

t=0

to maximize

∞

t=0



, n

; ξ



subject to the

aggregate Euler equation (16), agggregate labor supply (14), the evolution of µ

(12), the Phillips curve

(7), the evolution of Σ

(22)-(23) and the relationship between GDP and wages (15). In the RANK version

of our economy, σ = 0 and (22) is replaced by Σ

= 1 for all t. Appendix D presents the Lagrangian

associated with this problem along with the ﬁrst order necessary conditions for optimality.

5.1 Long run outcomes under the optimal Ramsey plan and the payroll subsidy

To proceed further, we need to take a stand on the value of the payroll subsidy τ. In RANK, if we imposed

a production subsidy to eliminate the distortions caused by market power, zero inﬂation is optimal in the

long run in the absence of aggregate shocks. This need not be true in our HANK economy where σ > 0

and so Σ

is endogenous. As in the standard NK model, the Phillips curve (7) implies a long-run trade-oﬀ

between inﬂation and economic activity:

(Π − 1)Π =

(1 −

βϑ

−1

)(1 − λ)Ψ



1 −

(1 − τ)λw



(25)

The presence of a long-run tradeoﬀ implies that the policymaker can move wages (or equivalently output)

above or below its ﬂexible-price level by persistently deviating from price stability. While it is not optimal

to do so in RANK, it may in fact be optimal in HANK because the level of economic activity aﬀects both

the amount of income risk households face w

and their ability to self-insure against this risk, µ

. For

example, if income risk is countercyclical, Θ > 1 the planner may want to create inﬂation to raise wages

(and output) above the level consistent with productive eﬃciency (w > 1), and thereby reduce income risk.

To make our results as comparable as possible to the classic NK literature on optimal monetary policy,

we eliminate this motive for deviating from price stability by introducing an appropriately chosen payroll

subsidy τ . To see how this works, consider the case with countercyclical risk in which the planner wants

to implement a high after-tax wage w > 1 in the long run in order to reduce inequality. From (25) it is

easy to see that if τ =

λ−1

(the standard subsidy used in the RANK literature, such a high level of wages

entails a marginal cost greater than 1 which implies positive long run inﬂation Π > 1. However, if the

payroll subsidy is larger, the steady state marginal cost can be brought down to 1, consistent with zero

inﬂation in the long run.

More generally, Appendix D.1 shows that in the presence of an appropriately chosen payroll subsidy to

ensure zero inﬂation Π = 1, the planner’s ﬁrst-order condition for wages - which states that the net-beneﬁt

of higher economic activity must be zero at an optimum - becomes:

Ω

|{z}

beneﬁt from

reduction of

inequality

≡

(1 −

β)(1 − Λ)

| {z }

reduction of inequality

due to low interest rates

Θ − 1

(1 −

β)(1 − Λ)

| {z }

reduction of inequality

due to high output

w − 1

1 + γρw

| {z }

cost of deviating

from productive eﬃciency

(26)

Equation (26) implies that the steady state wage and payroll subsidy consistent with the optimality of zero

long-run inﬂation satisfy:

w =

1 + Ω

1 − γρΩ

and τ =

λ − 1

1 + γρ

Ω

Ω + 1

(27)

Ω summarizes the beneﬁt from a reduction in consumption inequality due to higher economic activity. The

planner has the option to reduce interest rates and raise output above the ﬂexible price level. Equation

(27) states that at an optimum, the marginal beneﬁt of lower inequality due to lower rates and higher

output, Ω, must equal the marginal cost of distorting productive eﬃciency by raising output (and wages)

above the ﬂexible price level which is proportional to w − 1, the negative of the labor-wedge.

Absent uninsurable risk (Λ = 0, Θ = 1), there is no inequality and so there is no beneﬁt from higher

economic activity in terms of reducing inequality, Ω = 0. Consequently, in RANK, optimal policy equates

the cost of deviating from productive eﬃciency in steady state to 0 and hence w = 1 in the long run. In

this case, Π = 1 in steady state can be implemented with the standard RANK subsidy τ =

λ−1

(from eq.

(27)) which removes the monopolistic distortion.

In the presence of risk (Λ > 0), optimal monetary policy seeks to reduce consumption inequality. This

can be accomplished both by reducing labor income risk w

and by making it easier for households to

self-insure against this risk (by reducing µ

). Thus the policymaker may want to deviate from productive

eﬃciency and price stability, both to facilitate self-insurance and to reduce income risk; equation (26)

shows that Λ and Θ − 1 represent the strength of these two motives respectively.

Consider ﬁrst the self-insurance channel. When Θ = 1, income risk is acyclical: the level of economic

activity does not aﬀect household income risk. In this case, deviating from price stability and productive

eﬃciency (say by implementing a wage w > z = 1) delivers no beneﬁts in terms of lower income inequality

(second term on the LHS of (26) is zero). However, lowering real interest rates still makes it easier for

households to smooth consumption by borrowing and reduces the pass-through from income shocks into

consumption, measured by the ﬁrst term of the LHS, reducing consumption inequality. Lower interest

rates and the associated higher level of economic activity also have a cost, since they distort output and

employment above the productively eﬃcient level. Optimal policy equates these costs and beneﬁts. So,

even with acyclical risk, Ω > 0, and output is optimally above productive eﬃciency in the long run. Since

higher wages increase the ﬁrms marginal cost, it takes a higher payroll subsidy than in RANK τ >

λ−1

implement Π = 1 in steady state.

Next, consider the income risk channel. When Θ > 1, income risk is countercyclical: higher economic

activity lowers income risk. In this case, stimulating output above its productively eﬃcient level lowers

consumption inequality even for a ﬁxed µ; in addition, the lower interest rates necessary to implement

Note that here there is no term representing the cost of inﬂation, precisely because we assume that whatever the steady

state level of wages, the appropriate payroll subsidy is chosen so that ﬁrms’ marginal costs are consistent with zero inﬂation

in the long-run, i.e., (25) holds with Π = 1.

higher output reduce µ further reducing consumption inequality. Thus, the beneﬁt from higher output is

even larger than if Θ = 1 - both LHS components in (26) are positive and Ω is larger - and so output (and

wages) must be even further above the productive eﬃcient level than if Θ = 1. Again, it takes a higher

payroll subsidy τ >

λ−1

to implement Π = 1 in steady state.

In contrast, when risk is procyclical (Θ < 1), the eﬀect of higher economic activity and lower rates on

consumption inequality are ambiguous. While lower rates decrease the passthrough from income shocks to

consumption (Λ > 0), they also raise output which now increases income risk (Θ − 1 < 0). For suﬃciently

procyclical risk, the second eﬀect dominates, Ω < 0 and the optimal steady state level of output (and

wages) is below the productively eﬃcient level. In this case, it takes a lower payroll subsidy than

λ−1

implement Π = 1 in steady state. For mildly procylical risk, the self-insurance channel dominates and

Ω > 0 with w > 1 in steady state. The self-insurance channel is perfectly balanced by the income risk

channel if 1 − Θ = Λ in which case Ω = 0; higher economic activity and low interest rates have no ﬁrst

order eﬀect on consumption inequality and in this case, the planner does not wish to distort productive

eﬃciency in steady state, setting w = 1. The Ω = 0 case will be a useful benchmark in what follows.

Remark 1 (Comparison with Zero-Liquidity Limits). The self-insurance channel is absent in models which

feature incomplete markets but impose the zero liquidity limit such as Bilbiie (2019a,b); Ravn and Sterk

(2017); Challe (2020) and others. Zero liquidity implies that in equilibrium, the passthrough from income

risk to consumption risk is invariant to policy since it always equals 1. Instead, our analysis emphasizes

that in HANK economies interest rate policy aﬀects welfare not just via its eﬀect on the level of economic

activity, as in RANK, but also by aﬀecting the ease with which households can self-insure.

As is standard in the NK literature, a useful benchmark is the level of output under ﬂexible prices. In

a ﬂexible-price version of the HANK economy, we would have w

= wz

at all times, and output would be

= z

ρ (ln w + ln z

) +

1 + γρz

while the eﬃcient level of output is:

= z

ρ ln z

1 + γρz

In RANK, the ﬂexible-price and eﬃcient levels of output coincide: y

= y

. This is also true in HANK with

Ω = 0. But in general, when Ω 6= 0, the ﬂexible-price and eﬃcient levels of output no longer coincide. With

strongly procyclical risk Ω < 0, the ﬂexible-price level of output y

is always below its eﬃcient level y

while with mildly procyclical or countercyclical risk Ω > 0, y

is always above y

. Using these deﬁnitions,

we can express the linearized version of the Phillips curve (7) as:

t+1

+ κ (by

− by

) (28)

where κ =



1+γρ

ρΨ



λ−1

, by

ρ+1

1+γρ

and by

ρ+y

1+γρ

5.2 Calibration

While our results are primarily analytical, when plotting IRFs we parameterize the model as follows.

We choose

ξ to normalize aggregate steady state output y

∗

to 1 in the HANK economy with Ω = 0

(equivalently, in the RANK economy). We calibrate the model to an annual frequency and choose the

standard deviation of ξ

(i), σ, so that the standard deviation of income in steady state equals 0.5.

This

is in line with Guvenen et al. (2014) who using administrative data ﬁnd the standard deviation of 1 year

log earnings growth rate to be slightly above 0.5. We set the slope of the Phillips curve κ = 0.01, and the

elasticity of substitution between varieties

λ−1

to 10, implying a 10 percent steady state markup, λ = 1.1.

We set the coeﬃcient of relative prudence for the median household, −

000

(c)

= γ, to be 3, within the range

of estimates in the literature (see e.g. Cagetti (2003); Fagereng et al. (2017); Christelis et al. (2015)). We

set r = 4%. ρ can be interpreted as the Frisch elasticity of labor supply for the median household; we set it

equal to 1/3, within the range of estimates from the micro literature. We set the persistence of the shock

= 0.8. Following Nistic`o (2016), we set ϑ = 0.85. Finally, we consider two values for the cyclicality of

income risk: φ = γ (which implies Ω = 0), and φ = −3 (which implies Ω > 0 and countercyclical risk).

Finally, we set ξ = 1 + γρ to normalize the eﬃcient level of output in steady state to 1.

5.3 Dynamics under optimal monetary policy under RANK

As is common in the NK literature, we characterize optimal policy by linearizing the ﬁrst order conditions

arising from the planner’s Lagrangian (presented in Appendix E). It is useful to compare this characteri-

zation to optimal policy in a RANK version of our economy.

Lemma 1 (Optimal monetary policy in RANK). In RANK (Λ = 0, Θ = 1), output and inﬂation {by

, π

}

∞

t=0

under optimal policy satisfy

= by

− by

(29)

= η

t−1

−

λ − 1

(30)

t+1

+ κ (by

− by

) (31)

where η

is the (normalized) multiplier on the Phillips curve (7) and is deﬁned in Appendix E.1.

Proof. See Appendix E.1.

Combining (29)-(30), we see that optimal policy in RANK satisﬁes the standard target criterion:

(by

− by

) −



t−1

− by

t−1



λ − 1

= 0 (32)

where by

−1

= by

−1

= 0. Combining this with (31) and using the fact that by

= by

in RANK, we see that the

economy features a divine coincidence: it is both feasible and optimal for monetary policy to set by

= by

and π

= 0 at all dates and states. Given the appropriate steady state subsidy τ =

λ−1

, the ﬂexible-price

level of output, which is also consistent with zero inﬂation, maximizes social welfare –there is no tradeoﬀ

between implementing the eﬃcient level of output and price stability.

The standard deviation of income is given by (1 − γρµw)wσ. We calibrate all parameters except the cyclicality of income

risk to an economy with Ω = 0, which implies w = 1.

See for example, chapter 5 in Gal´ı (2015).

5.4 Dynamics of monetary policy under HANK

In HANK, the planner has an additional objective relative to RANK: in addition to stabilizing inﬂation

and keeping output close to its eﬃcient level, she wants to keep inequality Σ

as low as possible. The

innovations to inequality depend on consumption risk µ

which in turn depends on both income risk σ

and the pass-through µ

. This can be seen from the linearized version of (22) which is given by:











γ (1 − Θ) by

+ Λbµ

| {z }

consumption

risk

βR

t−1

for t > 0

γ (1 − Θ) by

+ Λbµ

ϑΛΣ

1−ϑ

bµ

for t = 0

(33)

One way to reduce consumption inequality is to aﬀect the level of output: with procyclical risk (Θ < 1)

lower output directly reduces income risk (Θ > 1) faced by households while with countercyclical risk,

a higher level of output is necessary to reduce income risk. An alternative path to lower consumption

inequality is to commit to a lower path of interest rates which reduces pass-through from income to

consumption risk.

However, the planner only has one instrument - the nominal interest rate. Lowering the nominal interest

rate lowers the pass-through from income risk to consumption risk (measured by µ

) but increases output.

If risk is countercyclical Θ > 1, then this too reduces consumption risk. However, if risk is procyclical

Θ < 1, then it increases income risk, leaving the overall eﬀect on consumption risk unclear. To see what

combinations of {by

, bµ

} that the planner can implement with some path of nominal interest rates, combine

the IS equation (19), µ recursion (20) using the deﬁnition of GDP (21) and solve forwards:

1 +



1 −



Ω

+ bµ



1 −



(1 + Ω)

γy

y + ρ

∞

s=0

(1 − Λ)

t+s

≡ Γ

(34)

where Γ

is an exogenous process driven by the sequence {y

}, which in turn depends solely on {bz

5.4.1 HANK with Ω = 0

To understand the trade-oﬀs facing the planner, it is useful to consider the special case in which Ω = 0

(or equivalently 1 − Θ = Λ). Recall from (26) that this is the case in which the zero inﬂation steady state

features productive eﬃciency (Π = 1, w = 1). This benchmark features mildly procyclical risk: while this

may not be the empirically relevant case, it is a useful benchmark because in this case, the constraint

on the planner’s ability to aﬀect consumption inequality is particularly severe. Recall that when risk is

procyclical, the eﬀect of expansionary monetary policy on consumption inequality is generally ambiguous:

higher output reduces the level of income risk, but lower interest rates reduces the passthrough from income

to consumption risk. When Ω = 0, both these eﬀects exactly cancel each other out and consumption is

invariant to monetary policy to ﬁrst-order. To see this, note that (33) becomes:











Λ(γby

+ bµ

) +

βR

t−1

for t > 0

Λ(γby

+ bµ

) +

ϑΛΣ

1−ϑ

bµ

for t = 0

(35)

while (34) becomes:

γby

+ bµ

= Γ

(36)

Clearly, in this case, the planner cannot aﬀect the evolution of consumption risk for dates t > 0 which is

solely driven by exogenous shocks {y

}

t≥0

denoted Γ

in (36). Plugging in (36) into (35) shows that the

evolution of inequality after date 0 is governed completely by the exogenous sequence {Γ











ΛΓ

βR

t−1

for t > 0

ΛΓ

ϑΛΣ

1−ϑ

bµ

for t = 0

(37)

Again, while a cut in interest rates lowers bµ

, it increases output by

and hence income risk, leaving con-

sumption risk unchanged. A higher path of aggregate productivity {bz

} (which implies a higher path of

{by

}) increases consumption risk in this case and monetary policy cannot do anything to prevent it: higher

productivity tends to increase output and hence the level of income risk that households face but tighter

monetary policy, which would be needed to forestall the rise in output, tends to make µ higher which itself

increases consumption risk.

Even though changes in interest rates (and hence µ) cannot aﬀect consumption inequality after date

0, the planner can aﬀect consumption inequality at date 0 (and thus at all subsequent dates, because

depends on

t−1

). This is because monetary policy changes after date 0 are anticipated while the date

0 change in monetary policy is unanticipated. As described in section 4, an unanticipated cut in interest

rates (and hence µ

) eﬀectively redistributes from savers to borrowers. To be clear, since we have an

economy where agents hold real (and not nominal) claims, this is not because inﬂation redistributes date

0 real wealth from savers to borrowers: the date 0 distribution of real wealth is unaﬀected.

But the

distribution of consumption is aﬀected, as rich savers ﬁnd that they receive a lower return on their bond

holdings than they had anticipated while poor debtors ﬁnd that their interest payments are smaller than

they had expected.

In sum, while the planner seeks to reduce consumption inequality in addition to stabilizing prices and

the gap output and its ﬂexible-price level, this is not possible after date 0 since (to ﬁrst order) the evolution

of consumption inequality is unaﬀected by policy. Eﬀectively, then after date 0, the planner faces the same

trade-oﬀ between output and inﬂation as in the RANK economy. At date 0, it is possible to reduce

consumption inequality via a surprise cut in interest rates which exploits households’ unhedged interest

rate exposure. Thus, the planner has an additional motive to cut rates at this date. This is reﬂected in

the optimal design of monetary policy, as we now demonstrate.

Proposition 3 (Optimal monetary policy with Ω = 0). Output and inﬂation {by

, π

}

∞

t=0

under optimal

Section 6 discusses the case where households hold nominal debt.

policy satisfy







α (by

− δby

− χ) for t = 0

− by

for t ≥ 1

(38)

βR

t−1

−

λ − 1

(39)

t+1

+ κ(by

− by

) (40)

where α > 1, 0 < δ < 1 and χ > 0 are deﬁned in Appendix E.1 and η

is the (normalized) multiplier on the

Phillips curve (40).

Proof. See Appendix E.1.

Combining (38) and (39), we get the following target criterion for all dates t > 1:

(by

− by

) −

βR



t−1

− by

t−1



λ − 1

= 0 (41)

Comparing equations (32) and (41) shows that when Ω = 0 the target criteria in HANK and RANK for

t > 0 are almost identical (under complete markets we have βR = 1 so the former collapses to the latter).

This reﬂects that fact that monetary policy cannot aﬀect consumption risk at dates t > 0, and thus faces

the same tradeoﬀ as RANK. But this is not true at t = 0, where the target criterion is:

− δby

λ − 1

= χ (42)

Equation (42) shows that at time 0 optimal policy in HANK deviates from that in RANK in three ways.

First, it is optimal to create a boom at date 0. To see this most clearly, suppose that productivity is at its

steady-state value, so by

= bz

= 0 for all t. Even in this case, it is optimal to move away from by

= π

= 0

and implement an output boom by

> 0 which is accompanied by inﬂation π

> 0. This is because, as

discussed earlier, the evolution of Σ

is diﬀerent at date 0, compared to all other dates. A surprise cut

in interest rates at date 0 reduces consumption inequality–as is summarized by the last term of (37) for

t = 0. The constant term χ > 0 in the date-0 target criterion (42) reﬂects exactly this beneﬁt from cutting

rates and reducing inequality at date 0. This is not because it is infeasible to set by

= by

= 0 and π

= 0

in the HANK economy; this remains feasible, and it remains costly for the planner to deviate from this

benchmark. But the costs of doing so are balanced by beneﬁts of reducing consumption inequality via

a surprise interest rate cut. Note that the desirability of exploiting households’ unhedged interest-rate

exposure for redistribution (the URE channel) makes the Ramsey plan time-inconsistent. Suppose that

the planner has been following a Ramsey plan since t = −∞ and the economy has converged to steady

state. Given the opportunity to deviate from this plan at date 0, the planner would do so, lowering interest

rates temporarily - i.e. the continuation of a Ramsey plan is not a Ramsey plan.

Second, whereas in RANK, optimal policy seeks to move output by

one-for-one with its eﬃcient level

(= by

in RANK), which ﬂuctuates due to productivity shocks, under HANK it is optimal to track the

ﬂexible-price level of output by

less than one-for-one. In other words, 0 < δ < 1 in (42). Figure 1 depicts

the optimal level of date 0 output as a function of ﬂexible-price level of output by

in HANK and RANK.

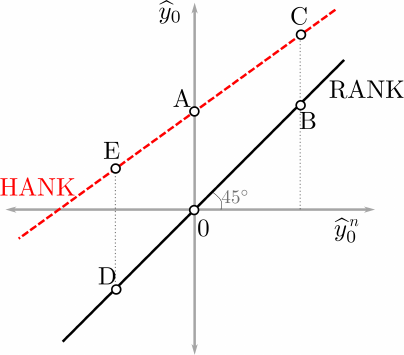
Figure 1. Optimal level of by

in HANK (Ω = 0) and RANK absent markup shocks

First, suppose, by

= 0. In RANK, it is optimal to track this and to set by

= by

= 0. But in HANK there

is a ﬁrst order beneﬁt from cutting interest rates to reduce inequality, creating a boom in output, until

the marginal beneﬁt of an additional reduction in nominal rates is outweighed by the cost of distorting

output further above its eﬃcient level (point A in Figure 1). Next, suppose that by

> 0. Again, the

RANK planner sets by

= by

(denoted by point B in the Figure). If the HANK planner were also to set

= by

> 0, this would already generate a surprise fall in interest rates, which would reduce inequality to

some extent. The HANK planner still perceives some additional beneﬁt to reducing inequality further but

the marginal beneﬁt is smaller since inequality has already been reduced. Consequently, it is not optimal

to deviate as much from productive eﬃciency as in the case by

= 0, and so the gap between points C and

B is smaller than that between points A and the origin. Conversely, when by

< 0, tracking the ﬂexible

price allocation would entail a surprise interest rate increase which would increase consumption inequality.

The beneﬁt of deviating from this RANK allocation is larger in this case and therefore it is optimal to

tolerate a larger deviation from production eﬃciency: the gap between points D and E is larger than that

between point A and the origin.

Finally, the date 0 target criterion puts less weight on inﬂation relative to output α > 1. This is because,

given the constraint on monetary policy imposed by (36), the evolution of consumption inequality depends

directly on the sequences {by

, by

}

∞

t=0

but not on inﬂation. Thus, the target criterion puts relatively less

weight on inﬂation and more on output, which attains heightened importance due to its eﬀects on inequality.

Figure 2 shows the dynamics of optimal policy absent shocks in the economy with Ω = 0. The policy

maker cuts nominal interest rates at date 0 (panel d), which generates a fall in real rates and in the

passthrough from income risk to consumption risk µ

(panel e). The fall in consumption risk in turn

reduces consumption inequality on impact (panel c), after which it gradually returns to steady state. The

fall in interest rates also generates a boom in output (panel a) and inﬂation (panel b). Since there are no

shocks to the eﬃcient level of output in this scenario, both the boom in output and increase in inﬂation

are in themselves undesirable from an eﬃciency perspective, even if they are a price worth paying for

a persistent reduction in inequality. In order to arrest the increase in inﬂation, the planner commits to

tighten policy, generating a fall in output and deﬂation, from date 1 onwards. Since ﬁrms are forward

looking, a commitment to lower inﬂation in the future mitigates the date 0 inﬂation caused by the boom

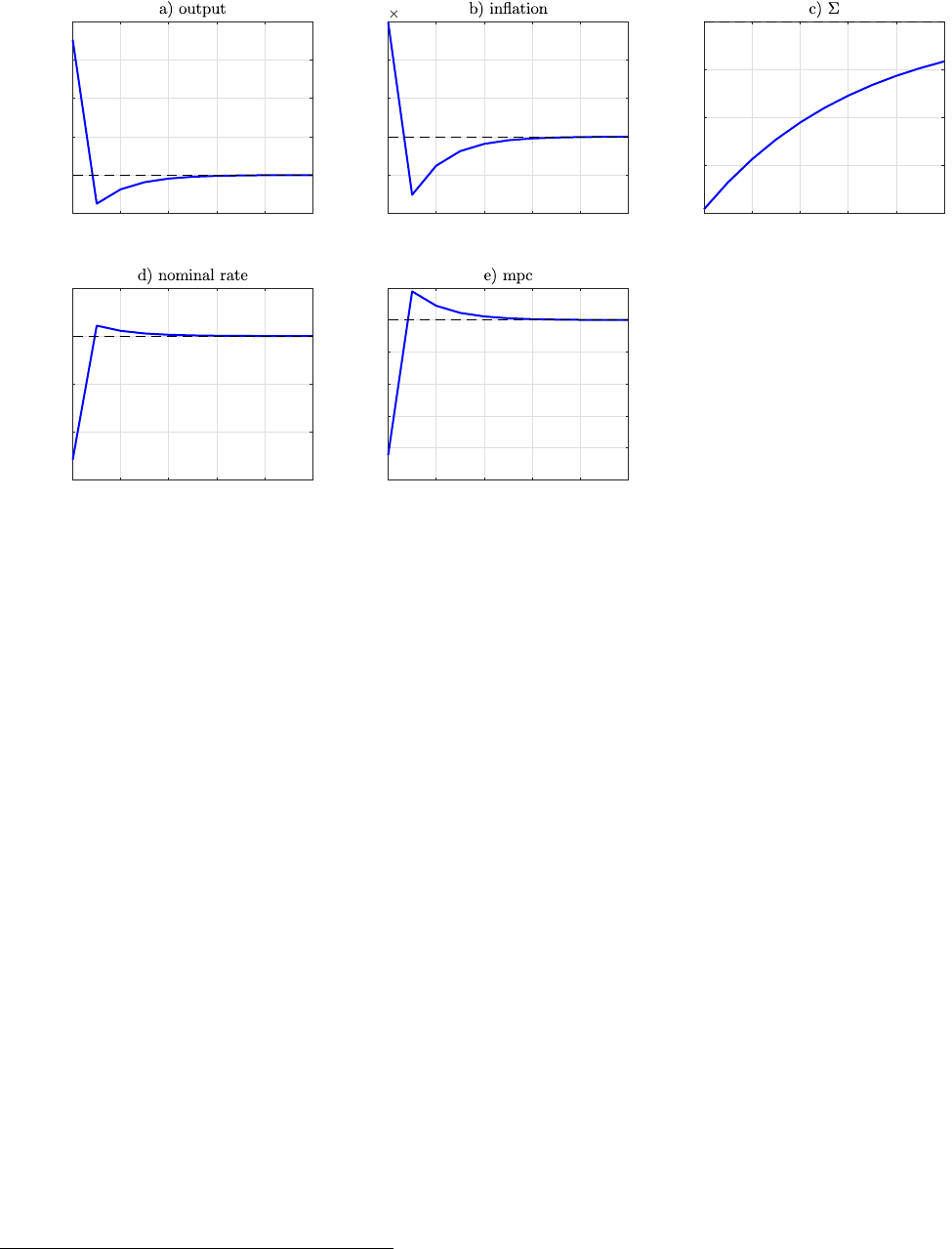
0 2 4 6 8 10

-0.02

0.02

0.04

0.06

0.08

0 2 4 6 8 10

-2

-1

-3

0 2 4 6 8 10

-0.02

-0.015

-0.01

-0.005

0 2 4 6 8 10

-0.3

-0.2

-0.1

0.1

0 2 4 6 8 10

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

Figure 2. Time Inconsistency: Optimal dynamics absent shocks. All variables are plotted as percentage deviations from

their steady state values.

in output.

Next, we discuss the optimal dynamic response of the economy to a negative productivity shock. Figure

3 shows the impulse responses to a negative productivity shock under optimal policy in the HANK and

RANK models, deﬁned as the diﬀerence between outcomes with and without the shock. That is, for any

variable of interest x, we plot x

=−0.01

−x

In the RANK economy (red lines), the planner allows

output to fall (panel a) in line with the natural rate of output, keeping the output gap (panel f) and

inﬂation (panel b) equal to zero. Implementing a fall in output requires an increase in nominal interest

rates (panel d), but since agents do not face idiosyncratic risk, this has no eﬀect on consumption inequality

which is always zero.

In the HANK economy (blue lines), a sharp increase in interest rates would increase the passthrough

from income to consumption risk and would persistently increase inequality. To avoid this, the planner

actually cuts interest rates at date 0, dampening the increase in passthrough µ

and the increase in

inequality. Output does not fall as much as the ﬂexible price level of output (as shown by the output gap

in panel f), and as a result inﬂation increases at date 0 - even relative to the scenario absent shocks. This

increase in inﬂation is not costless. To mitigate its impact, the planner commits to a slightly higher path

of interest rates, and lower output and inﬂation, from date 1 onwards.

Understanding the forces generating time inconsistency The diﬀerence in the optimal target

criterion than at all other dates arises only because there is existing wealth inequality at the start of date

0. Suppose that there is an equalization of asset positions across all households at the beginning of date 0.

In the RANK economy, the impulse response is identical to the response of the economy to the shock, since in the absence

of shocks, optimal policy keeps all variables at their steady state values and all deviations from steady state equal zero. This

is not true in the HANK economy, where (as shown in Figure 2) the Ramsey planner deviates from steady state even absent

shocks.

0 2 4 6 8 10

-0.04

-0.03

-0.02

-0.01

0 2 4 6 8 10

-4

-2

-4

0 2 4 6 8 10

-1

-0.5

0.5

1.5

-3

0 2 4 6 8 10

-0.03

-0.02

-0.01

0.01

0.02

0 2 4 6 8 10

0.01

0.02

0.03

0.04

0.05

0.06

0 2 4 6 8 10

-5

-3

Figure 3. HANK (Ω = 0) vs RANK optimal response to a negative productivity shock. Red line denotes RANK while

blue line represents HANK (Ω = 0). All variables are plotted as percentage deviations from their steady state values. In panel

f), we plot output gap as the diﬀerence between y

and y

normalized by steady state y: (by

/y) − (by

/y).

In this scenario, the URE channel is inoperative, as discussed in section 4 and surprise changes in µ

have

no additional eﬀect relative to anticipated changes. When there is existing wealth inequality, a surprise cut

in the path of interest rates (lower µ

) lowers the consumption of rich savers and raises the consumption

of poor borrowers, reducing consumption inequality. Consequently, at t = 0, the planner deviates from the

date t > 1 target criterion by cutting interest rates do engineer precisely this outcome. Absent existing

wealth inequality at the beginning of date 0, clearly there are no borrowers and savers to redistribute

between and this motive is absent. In fact, with Ω = 0, absent initial wealth inequality, equation (37)

becomes:

= ΛΓ

βR

t−1

∀t ≥ 0 (43)

with

−1

= −

βR



1−ϑ

1−ϑe



< 0. Equation (43) shows that without initial wealth inequality, the planner

is unable to aﬀect Σ

at any date (up to ﬁrst-order). Unsurprisingly then, the planner faces the standard

trade-oﬀ between price stability and productive ineﬃciency. Consequently, the optimal target criterion at

all dates in this case simpliﬁes to:

(by

− by

) −

βR



t−1

− by

t−1



λ − 1

= 0 (44)

with by

−1

= by

−1

= 0 and so divine coincidence holds - optimal policy implements π

= 0 and by

= by

at all

dates t ≥ 0 in response to productivity shocks.

Remark 2 (The interest rate exposure channel versus the Fisher channel). Previous research has shown

how the redistribution of wealth through inﬂation when assets and liabilities are nominal may create an

inﬂationary bias on the part of the central bank. This “Fisher channel” is absent in our baseline economy

where households only hold real assets: the planner is unable to redistribute real wealth via surprise inﬂa-

tion. Nonetheless, the planner can redistribute consumption via a surprise cut in the path of real rates via

the interest rate exposure channel (Auclert, 2019). Auclert (2019) studies how both these channel mediate

the eﬀect of interest rate changes on aggregate consumption in an environment with MPC heterogeneity.

In our economy, all agents have the same MPC, so monetary policy does not aﬀect aggregate consumption

through these channels. However, it does aﬀect the distribution of consumption and in our baseline econ-

omy, optimal monetary policy deliberately utilizes the interest rate exposure channel to reduce consumption

inequality. In Section 6, when we introduce nominal bonds into our model, optimal monetary policy exploits

both channels to achieve the same ends.

5.4.2 Optimal policy with countercyclical risk

While the case with Ω = 0 is a useful benchmark to understand the forces driving optimal monetary policy,

the empirically relevant case is one of countercyclical risk, which implies that Ω > 0.

In this case a cut in

interest rates, and the associated boom in output (and wages), reduce consumption risk through both the

income risk and self-insurance channels. With Ω = 0, risk was procyclical, and the beneﬁt of lower interest

rates (which lower µ and increase households’ ability to self insure) was exactly balanced by the cost of

the associated boom in output which increased the level of income risk faced by households. In contrast,

when risk is countercyclical, the increase in output actually reduces the level of income risk, at the same

time as lower interest rates improve households’ ability to self-insure: expansionary policy unambiguously

reduces consumption risk and inequality. This can be seen by substituting (34) into (33):











−γ



1 −



Ωby

+ ΛΓ

βR

t−1

for t > 0

−γ



1 −



Ωby

+ ΛΓ

ϑΛΣ

1−ϑ

bµ

for t = 0

(45)

When Ω > 0, an increase in output by

reduces the consumption risk faced by households at any date,

not just at date 0:

∂

∂ ˆy

< 0. In this environment, the planner would only refrain from increasing output

if doing so distorts productive eﬃciency and creates inﬂation. Indeed recall from (26) that in steady state

with Ω > 0, the marginal beneﬁt of reducing inequality by stimulating demand is exactly balanced by

the cost of deviating further from production ineﬃciency. The reason a marginal increase in output has a

ﬁrst-order cost in terms of productive eﬃciency is that the steady state in this case features an ineﬃciently

high level of output y > 1 (also reﬂected in w > 1). Out of steady state the planner faces a similar trade-oﬀ

between the beneﬁt of reducing inequality via higher output and the cost of further distorting productive

eﬃciency, while also seeking to limit deviations from price stability. This tradeoﬀ informs the optimal

design of monetary policy, as we discuss next.

More precisely, countercyclical risk (Θ > 1) implies Ω >

(1−

β)(1−Λ)

> 0. When 0 < Ω <

(1−

β)(1−Λ)

, risk is weakly

procyclical so expansionary monetary policy reduces pass through than it increase income risk, reducing consumption risk in

net.

Proposition 4 (Optimal monetary policy with countercyclical risk). Output and inﬂation {by

, π

}

∞

t=0

under optimal policy satisfy







(Ω)



− δ

(Ω)by

− χ(Ω)



for t = 0

α(Ω)



− δ(Ω)by



for t ≥ 1

(46)

βR

t−1

−

λ − 1

yπ

(47)

t+1

+ κ(by

− by

) + u

(48)

where α(Ω), δ(Ω), α

(Ω), δ

(Ω) and χ(Ω) are deﬁned in Appendix E.1 and satisfy α

(0) = α, δ

(0) = δ,

χ(0) = χ, α(0) = 1, δ(0) = 1. Further, when risk is countercyclical α(Ω), α

(Ω) > 1 and δ(Ω), δ

(Ω) < 1.

Proof. See Appendix E.1.

By combining (46) with (48), one can derive the optimal target criterion for t = 0:



− δ

(Ω)by



λ − 1

(Ω)

= χ(Ω) for t = 0 (49)

and for dates t > 1:



− by

t−1



− δ(Ω)



− by

∗

t−1



λ − 1

α(Ω)

= 0 (50)

As in the case Ω = 0, optimal policy deviates from RANK at date 0, creating a boom even absent

exogenous shocks. However, unlike in the case Ω = 0, with countercyclical risk optimal policy also deviates

from the RANK target criterion at subsequent dates t > 1. This should not be not surprising: with Ω = 0,

monetary policy can only aﬀect the evolution of consumption inequality (to ﬁrst order) at date 0. However,

with countercyclical risk, an expansion in output reduces inequality at all dates, so monetary policy faces

a tradeoﬀ between the beneﬁts of lower inequality and the cost of distorting productive eﬃciency and

price stability at all dates, and deviates from RANK as a result. In particular, δ(Ω) < 1 when risk is

countercyclical: output tracks the ﬂexible price level of output less than one for one at all dates. In

addition, α(Ω) > 1: the planner puts more weight on stabilizing output relative to inﬂation at all dates.

To understand why output moves less than one-for-one with its ﬂexible price level at all date, δ(Ω) < 1,

recall the distinction between three diﬀerent levels of output: the productively eﬃcient level of output y

the ﬂexible price level of output y

, and the equilibrium level of output y

. When Ω = 0, y

= y

. In

this case, the standard subsidy corrects for the distortion due to monopolistic competition, and productive

eﬃciency is obtained when there is zero inﬂation at all dates, or when prices are ﬂexible. In other words, the

ﬂexible price version of the economy with Ω = 0 features a zero labor wedge at all dates, T

≡ ln z

−ln w

= 0

where w

denotes the wage consistent with the ﬂexible price level of output.

However, with countercyclical risk, Ω > 0, and the ﬂexible price level of output y

is higher than the

eﬃcient level of output y

, whatever the level of productivity. In this case, ﬁrms enjoy a subsidy which is

larger than the one necessary to eliminate the distortion due to monopolistic competition (see eq. (27)), and

output would be ineﬃciently high under ﬂexible prices. The ﬂexible price version of this economy features

a negative labor wedge - a net subsidy to output and employment - at all times. Consequently keeping

0 2 4 6 8 10

-0.04

-0.03

-0.02

-0.01

0 2 4 6 8 10

-5

-4

0 2 4 6 8 10

-2

-3

0 2 4 6 8 10

-0.03

-0.02

-0.01

0.01

0.02

0 2 4 6 8 10

0.01

0.02

0.03

0.04

0.05

0.06

0 2 4 6 8 10

-5

-3

Figure 4. HANK (Ω > 0) vs RANK optimal response to a negative productivity shock. Red line denotes RANK, blue

line represents HANK with countercyclical risk (Ω > 0), and gray line represents HANK with Ω = 0. All variables are plotted

as percentage deviations from their steady state values. In panel f), we plot output gap as the diﬀerence between y

and y

normalized by steady state y: (by

/y) − (by

/y).

output equal to its ﬂexible price level entails keeping output ineﬃciently high at all times. Conversely,

in order to set output equal to its eﬃcient level, and undo the eﬀects of the net subsidy to output and

employment, one would have to drive output y

down below its ﬂexible price level y

Absent shocks, the planner could always implement the eﬃcient level of output by raising interest

rates above their steady state level, reducing output below its ineﬃciently high ﬂexible price level, and

eliminating the negative labor wedge. She chooses not to do this, however, because the cost in terms of

increased consumption inequality is too high - so she sets output equal to its ﬂexible price level.

Now consider a scenario in which productivity is higher than in steady state (z > 1). In this case, the

planner could continue to set output equal to its ﬂexible price level, keeping the labor wedge unchanged

= ln z

− ln w

= −ln w < 0). This would entail increasing y

one for one with y

. But it is no

longer optimal to do so. The only reason the planner does not eliminate the ineﬃcient subsidy in steady

state is that doing so would increase inequality too much. Now however, with higher output, consumption

inequality is already lower, and the beneﬁt of the ineﬃcient subsidy is lower: even if the planner were

to implement a lower level of output relative to the ﬂexible price level, improving productive eﬃciency,

inequality would still be relatively low. Optimal policy seeks to reduce the magnitude of the labor wedge

by bringing the level of output y

closer to the eﬃcient level of output y

. Since 1 = y

< y

= y in steady

state, this entails by

< by

Conversely, suppose productivity falls relative to steady state, z < 1. Again, the planner could track

the ﬂexible price level of output y

, keeping the labor wedge unchanged. Doing so would entail reducing

output one for one with the ﬂexible price level of output. But when output is lower, consumption inequality

is higher. In this case, the rationale for keeping output above its eﬃcient level y

is not eliminated - it

is actually strengthened. It is optimal to deviate even further from productive eﬃciency, increase the

eﬀective subsidy to output and employment, and reduce output less than one for one with the eﬃcient

level of output.

Figure 4 shows the impulse responses to a negative productivity shock under optimal policy in HANK

with countercyclical risk (blue lines), with outcomes in RANK (red lines) and HANK with Ω = 0 (gray

lines) shown as benchmarks. As in the benchmark with Ω = 0, the planner deviates from optimal policy in

RANK - which tracks the ﬂexible price level of output - by cutting nominal interest rates at date 0 (panel

d) and mitigating the fall in output (panel a) on impact, at the cost of creating an increase in inﬂation

(panel b). Recall that in the economy with Ω = 0, the planner attempted to dampen this increase in

inﬂation by committing to tighter policy starting at date 1. With countercyclical risk, however, any fall

in output is costly because it directly increases inequality. Indeed, even under optimal policy, the path of

inequality is higher with countercyclical risk (panel c). To prevent inequality from rising even more, the

planner postpones the commitment to tighter policy in the future. While interest rates still rise at date 1

(blue line in panel d), the increase is smaller than in the RANK economy (red line) or the HANK economy

with Ω = 0 (gray line). As a result, the fall in inﬂation and output-gap are also smoothed out over time.

Remark 3 (The role of initial wealth inequality with countercyclical risk). With countercyclical risk

(Ω > 0), the optimal target criterion is diﬀerent at date t = 0 and at all subsequent dates, as was the case

when Ω = 0. In particular, optimal policy features a boom at date 0 even absent exogenous shocks. As in

the Ω = 0 case, such a policy is optimal because given existing wealth inequality at date 0, a surprise cut

in interest rates raises the consumption of poor borrowers and reduces the consumption of rich savers. To

understand the role of wealth inequality in driving this result, suppose again that there is an equalization

of household wealth at the beginning of date 0. In this case, the optimal target criterion (50) characterizes

optimal policy at all dates (with by

−1

= by

∗

−1

= 0). This implies that absent shocks, the planner keeps interest

rates at their steady state value. However, unlike in the case with Ω = 0 and wealth equalization, it is no

longer optimal to implement zero inﬂation and replicate ﬂexible price allocations in response to productivity

shocks - even though it remains feasible to do so.

Figure 5 plots dynamics under optimal policy in this scenario. Qualitatively, policy is similar to the

case without wealth equalization in which there is a time inconsistency problem. Relative to RANK, the

planner implements a lower increase in interest rates on impact (panel d), resulting in a lower increase

in output (panel a) and the passthrough from income to consumption risk µ

(panel e). This comes at the

cost of a short-lived increase in inﬂation. Note that inequality (shown in the panel c) is below its steady

state level, despite the increase in income risk caused by the fall in output, because the initial equalization

of wealth reduces consumption inequality at the start of date 0.

6 Nominal debt

So far we have considered an economy in which households traded inﬂation indexed bonds. As mentioned

in Remark 2, we made this assumption to distinguish between two ways in which monetary policy can

aﬀect the distribution of consumption in HANK economies. The ﬁrst is the interest rate exposure channel:

an unanticipated fall in real interest rates increases the consumption of poor debtors and reduces that of

rich savers. The second is the Fisher eﬀect: unanticipated inﬂation redistributes real wealth from savers

0 2 4 6 8 10

-0.04

-0.03

-0.02

-0.01

0 2 4 6 8 10

-2

-4

0 2 4 6 8 10

-0.1

-0.08

-0.06

-0.04

-0.02

0 2 4 6 8 10

0.005

0.01

0.015

0.02

0 2 4 6 8 10

0.01

0.02

0.03

0.04

0.05

0.06

0 2 4 6 8 10

-2

-3

Figure 5. HANK (Ω > 0) vs RANK optimal response to a negative productivity shock in the economy with wealth

equalization at the beginning of date 0. Red line denotes RANK, blue line represents HANK with countercyclical risk (Ω > 0).

All variables are plotted as percentage deviations from their steady state values. In panel f), we plot output gap as the

diﬀerence between y

and y

normalized by steady state y: (by

/y) − (by

/y).

who hold nominal assets to debtors with nominal liabilities. Our baseline model with inﬂation indexed

debt abstracts altogether from the second eﬀect to focus on the ﬁrst. In this section, we allow households

to trade nominal debt and show how the the presence of the Fisher eﬀect changes the optimal conduct of

monetary policy.

Financial intermediaries now trade nominal claims at nominal price

1+i

which pay a dollar tomorrow.

Then the household’s budget constraint can be written as:

(i) +

1 + i

t+1

(i) = P

(i) + A

(i) + P

where A

t+1

(i) is the quantity of nominal claims purchased by the household at date t. The details of this

extension are in Appendix F. As before the evolution of this economy is characterized by the aggregate IS

equation (11), the evolution of µ(12), Phillips curve (7), the deﬁnition of GDP (15) and the evolution of

Σ, replacing R

1+i

t+1

. Four of these ﬁve equations are unaﬀected by the introduction of nominal bonds

- the exception is the evolution of Σ, which becomes:

ln Σ

+ ln [1 − ϑ + ϑΣ

t−1

] + I(t = 0) ln





1 − ϑe



−1







(51)

(51) shows that the presence of nominal debt means that unanticipated higher inﬂation reduces consump-

tion inequality. Since there are no aggregate shocks except at date 0 and the Ramsey planner can only

re-optimize at date 0, actual and expected inﬂation coincide in equilibrium except at date 0. As Appendix

See Appendix F for the derivation.

F details, the cohort born at date s < 0 enters date 0 with with a cross-sectional distribution of real

wealth which is N



0, −sw



−1





. Higher than expected inﬂation Π

> E

−1

compresses the

distribution of real wealth. Thus, by generating inﬂation at date 0, the planner can reduce wealth and

hence consumption inequality. This reduction in consumption inequality is in addition to the reduction

achieved by the surprise cut in interest rates at date 0.

0 2 4 6 8 10

-5

-3

0 2 4 6 8 10

-0.02

-0.01

0.01

0.02

0.03

0.04

0 2 4 6 8 10

-0.015

-0.01

-0.005

0 2 4 6 8 10

-0.08

-0.06

-0.04

-0.02

0.02

0 2 4 6 8 10

-0.06

-0.04

-0.02

0.02

Figure 6. Time inconsistency with nominal debt: Optimal dynamics absent shocks in alternative calibration (κ = 0.5).

Blue line denotes HANK with countercylcical risk and real debt, red line denotes HANK with countercyclical risk and nominal

debt. All variables are plotted as percentage deviations from their steady state values.

Qualitatively, this increases the planner’s incentive to create a boom at date 0 even absent aggregate

shocks. Quantitatively, though, this eﬀect is small in our baseline calibration, as Figure 8 in Appendix

F shows - optimal policy in the two economies is essentially identical. This is primarily because in our

baseline calibration, the Phillips curve is relatively ﬂat (κ = 0.01) which means that even a large cut in

real interest rates, and a large boom in output, generates only a small increase in inﬂation. In order to

generate a large enough increase in inﬂation to eﬀect signiﬁcant redistribution, it would be necessary to

engineer a massive deviation from the productively eﬃcient level of output, and it is not optimal for the

planner to do this.

To illustrate the qualitative eﬀect of introducing inﬂation-indexed debt, Figure 6 shows optimal policy

absent shocks with a steeper Phillips curve (κ = 0.5). As panel b shows, the planner creates a larger increase

in inﬂation in the economy with nominal debt (red line) than in the economy with inﬂation-indexed debt

(blue line). This results in a larger reduction in inequality (panel c). The black dashed line in this panel

shows the eﬀect of implementing the optimal policy from the economy with inﬂation-indexed debt in the

economy with nominal debt. Even if the planner follows this policy, and does not actively exploit the

Fisher eﬀect, this already automatically generates a larger reduction in inequality than in the economy

with inﬂation-indexed debt (the black dashed line is below the blue line) because the same increase in

inﬂation now redistributes real wealth. The planner actually generates a further increase in inﬂation, and

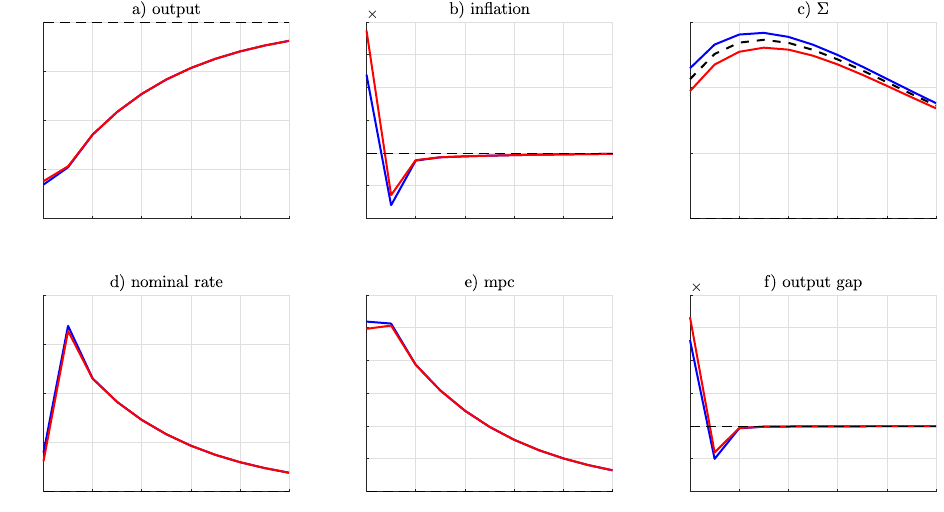
0 2 4 6 8 10

-0.04

-0.03

-0.02

-0.01

0 2 4 6 8 10

-4

-2

-3

0 2 4 6 8 10

0.005

0.01

0.015

0 2 4 6 8 10

0.005

0.01

0.015

0.02

0 2 4 6 8 10

0.01

0.02

0.03

0.04

0.05

0.06

0 2 4 6 8 10

-2

-1

-3

Figure 7. Nominal vs inﬂation indexed debt: optimal response to a negative productivity shock in alternative calibration

(κ = 0.5). Blue line represents HANK with countercyclical risk and real debt, red line denotes HANK with countercyclical

risk and nominal debt. All variables are plotted as percentage deviations from their steady state values. In panel f), we plot

output gap as the diﬀerence between y

and y

normalized by steady state y: (by

/y) − (by

/y).

so inequality falls even more (the red line is below the black dashed line).

The presence of nominal assets and liabilities also aﬀects the optimal response to shocks. Figure 7 plots

the impulse responses (deﬁned as in the previous section) to a negative productivity shock under optimal

policy in the alternative calibration with κ = 0.5. Allocations under optimal policy in the economy with

nominal debt (red line) are similar to those with inﬂation-indexed debt (blue line), even with a steep

Phillips curve. However, the level of output now deviates even more from y

(panel f) in order to generate

a larger surprise increase in inﬂation (panel b). This is optimal when risk is countercyclical because negative

productivity shock tends to increase inequality (panel c). Creating more surprise inﬂation partially oﬀsets

this, yielding a lower increase in inequality (red line) than would obtain if the planner followed the same

policy as in the economy with inﬂation-indexed debt (black dashed line). As in the previous ﬁgure, though,

even following this same policy would automatically generate a larger reduction in inequality than in the

economy with inﬂation-indexed debt (blue line).

7 Conclusion

We use a analytically tractable HANK model to study how monetary policy aﬀects inequality, and the

extent to which this warrants a change in the principles governing the design of monetary policy which have

been developed in the Representative Agent New Keynesian literature. In a complete markets economy,

monetary policy aﬀects output and inﬂation but, trivially, has no eﬀects on inequality (since households

can use Arrow securities to insure themselves, eliminating consumption inequality). In our incomplete

markets economy, monetary policy aﬀects consumption risk and inequality through four channels. The

ﬁrst is the income risk channel: when the idiosyncratic income risk faced by households is countercyclical,

expansionary monetary policy, by generating a boom in output, tends to reduce income risk and inequality.

More subtly, lower interest rates make it easier for households to self-insure against income shocks, reducing

consumption risk for a given level of income risk - the self-insurance channel. Finally, unexpected cuts in

interest rates redistribute consumption through an unhedged interest rate exposure channel, and unexpected

inﬂation redistributed real wealth through the Fisher channel. Thus, expansionary monetary policy can

reduce consumption inequality through all four of these channels.

Given that monetary policy has this power to reduce inequality, how and when should it be used? A

utilitarian planner trades oﬀ the beneﬁts of lower inequality against the costs of pushing up output and

inﬂation above their eﬃcient levels. In recessions, inequality is already high - in the relevant case with

countercyclical risk - so the marginal beneﬁt of reducing inequality is particularly high. Consequently,

optimal monetary policy is more accommodative in recessions relative in to a RANK benchmark: the

planner prevents output from falling as much as the eﬃcient level of output, even though this entails

higher inﬂation, because curtailing the fall in output also curtails the rise in inequality.

References

Acharya, Sushant and Keshav Dogra, “Understanding HANK: insights from a PRANK,” Staﬀ Reports

835, Federal Reserve Bank of New York February 2018.

Angeletos, George-Marios and Laurent Emmanuel Calvet, “Idiosyncratic Production Risk, Growth

and the Business Cycle,” Journal of Monetary Economics, 2006, 53, 1095 – 1115.

Auclert, Adrien, “Monetary Policy and the Redistribution Channel,” American Economic Review, 2019,

109 (6), 2333 – 2367.

, Matt Rognlie, and Ludwig Straub, “The Intertemporal Keynesian Cross,” Working Paper 25020

2018.

Bhandari, Anmol, David Evans, Mikhail Golosov, and Thomas J Sargent, “Inequality, Business

Cycles and Monetary-Fiscal- Policy,” Working Paper 24710, National Bureau of Economic Research

June 2018.

Bilbiie, Florin O., “Limited Asset Markets Participation, Monetary Policy and (Inverted) Aggregate

Demand Logic,” Journal of Economic Theory, May 2008, 140 (1), 162–196.

, “Monetary Policy and Heterogeneity: An Analytical Framework,” Working Paper, November 2019.

, “The New Keynesian Cross: Understanding Monetary Policy with Hand-to-Mouth Households,” Jour-

nal of Monetary Economics, 2019, Forthcoming.

and Xavier Ragot, “Optimal Monetary Policy and Liquidity with Heterogeneous Households,” Work-

ing Papers 2018.

Blanchard, Olivier Jean and Jordi Gal´ı, “Real Wage Rigidities and the New Keynesian Model,”

Journal of Money, Credit and Banking, 2007, 39, 35 – 65.

Caballero, Ricardo J., “Consumption Puzzles and Precautionary Savings,” Journal of Monetary Eco-

nomics, 1990, 25 (1), 113 – 136.

Cagetti, Marco, “Wealth Accumulation over the Life Cycle and Precautionary Savings,” Journal of

Business & Economic Statistics, 2003, 21 (3), 339–353.

Calvet, Laurent Emmanuel, “Incomplete Markets and Volatility,” Journal of Economic Theory, 2001,

98, 295 – 338.

Calvo, Guillermo A and Maurice Obstfeld, “Optimal Time-Consistent Fiscal Policy with Finite

Lifetimes,” Econometrica, 1988, 56 (2), 411–432.

Challe, Edouard, “Uninsured Unemployment Risk and Optimal Monetary Policy in a Zero-Liquidity

Economy,” American Economic Journal: Macroeconomics, April 2020.

Christelis, Dimitris, Dimitris Georgarakos, Tullio Jappelli, and Maarten van Rooij, “Con-

sumption Uncertainty and Precautionary Saving,” CSEF Working Papers 421, Centre for Studies in

Economics and Finance (CSEF), University of Naples, Italy December 2015.

Cui, Wei and Vincent Sterk, “Quantitative Easing,” Working Papers, UCL 2019.

Debortoli, Davide and Jordi Gal´ı, “Monetary Policy with Heterogeneous Agents: Insights from TANK

models,” Working Paper 2018.

den Haan, Wouter, Pontus Rendahl, and Markus Riegler, “Unemployment (Fears) and Deﬂation-

ary Spirals,” Journal of the European Economic Assocation, 2018, 16(5), 1281 – 1349.

Fagereng, Andreas, Luigi Guiso, and Luigi Pistaferri, “Firm-Related Risk and Precautionary Saving

Response,” American Economic Review, May 2017, 107 (5), 393–97.

Gal´ı, Jordi, Monetary Policy, Inﬂation, and the Business Cycle: An Introduction to the New Keynesian

Framework and Its Applications, Second Edition, Princeton University Press, 2015.

Gal´ı, Jordi, David Lopez-Salido, and Javier Valles, “Understanding the Eﬀects of Government

Spending on Consumption,” Journal of the European Economic Association, 2007, 5 (1), 227–270.

Guvenen, Fatih, Serdar Ozkan, and Jae Song, “The Nature of Countercyclical Income Risk,” Journal

of Political Economy, 2014, 122 (3), 621–660.

Kaplan, Greg, Benjamin Moll, and Giovanni L. Violante, “Monetary Policy According to HANK,”

American Economic Review, March 2018, 108 (3), 697–743.

Kekre, Rohan, “Unemployment Insurance in Macroeconomic Stabilization,” Working Paper 2019.

McKay, Alisdair and Ricardo Reis, “The Role of Automatic Stabilizers in the U.S. Business Cycle,”

Econometrica, January 2016, 84, 141–194.

and , “Optimal Automatic Stabilizers,” Working Paper 2019.

, Emi Nakamura, and Jon Steinsson, “The Power of Forward Guidance Revisited,” American

Economic Review, October 2016, 106 (10), 3133.

Nistic`o, Salvatore, “Optimal Monetary Policy And Financial Stability In A Non-Ricardian Economy,”

Journal of the European Economic Association, October 2016, 14 (5), 1225–1252.

Nu˜no, Galo and Carlos Thomas, “Optimal Monetary Policy with Heterogeneous Agents,” Working

Papers 1624, Banco de Espana November 2019.

Ravn, Morten O. and Vincent Sterk, “Job Uncertainty and Deep Recessions,” Journal of Monetary

Economics, 2017, 90 (C), 125–141.

and , “Macroeconomic Fluctuations with HANK & SAM: An Analytical Approach,” Journal of the

European Economic Association, Forthcoming.

Rotemberg, Julio J., “Monopolistic Price Adjustment and Aggregate Output,” Review of Economic

Studies, 1982, 49 (4), 517–531.

Wang, Neng, “Caballero Meets Bewley: The Permanent-Income Hypothesis in General Equilibrium,”

American Economic Review, June 2003, 93 (3), 927–936.

Werning, Ivan, “Incomplete Markets and Aggregate Demand,” Working Paper 21448, National Bureau

of Economic Research August 2015.

Appendix

A Proof of Proposition 1

The date s problem of an individual i born at date s can be written as:

max

(i),`

(i),b

t+1

(i)}

−

∞

t=s

(βϑ)

t−s



−γc

(i)

+ ρe

(i)−ξ

(i)]



s.t.

(i) + q

t+1

(i) = w

(i) + b

(i) + T

(52)

where b

(i) = 0 and w

= (1 − τ) ew

. The optimal labor supply decisions of houshold i is given by:

(i) = ρ ln w

− ργc

(i) + ξ

(i) (53)

and the Euler equation is given by:

−γc

(i)

= βR

−γc

t+1

(i)

(54)

where we have used the fact that q

. Next, guess that the consumption decision rule takes the form:

(i) = C

+µ

(i) (55)

where x

(i) = b

t−1

(i) + w



(i) − ξ



denotes “virtual cash-on-hand”. Notice that x

t+1

(i) is normally

distributed and so given the guess (55), c

t+1

(i) is also normally distributed with mean:

t+1

(i) = C

t+1

+ µ

t+1



(i) + w



ρ ln w



+ T

− (1 + ργw

) c

(i)



and variance:



t+1

(i)



= µ

t+1

Taking logs of (54) and using the two expressions above:

(i) = −

ln βR

−

ln E

−γc

t+1

(i)

= −

ln βR

+ E

t+1

(i) −



t+1

(i)



= −

ln βR

+ C

t+1

+ µ

t+1



(i) + w



ρ ln w



+ T

− (1 + ργw

) c

(i)



−

γµ

t+1

Combining the c

(i) terms and using (55), the above can be rewritten as:

t+1



(1 + ργw

) +

−1

t+1



+µ

(i)} = −

ln βR

+ C

t+1

+ µ

t+1



(i) + w



ρ ln w



+ T



−

γµ

t+1

(56)

Matching coeﬃcients:

= −

ϑµ

t+1

ln βR

ϑµ

t+1

+ µ





ρ ln w



+ T



−

t+1

γµ

t+1

(57)

−1

= (1 + ργw

) +

−1

t+1

(58)

Notice that (58) is the same as (12) in the main text. Next, in equilibrium, aggregate hours worked is

given by:

= ρ ln w

− γρC

+ ξ

and hence aggregate income is:

= w

+ T

= w

ρ ln w

− γρw

+ w

ξ + T

Using this in (57) and the fact that C

= y

yields equation (11) in the main text.

B Planner’s Objective function

B.1 Consumption is normally distributed within cohort

Given the consumption function (9) and the normality of shocks, to consumption of newly born in-

dividuals at any date s is normally distributed with mean y

and variance σ

(s, s) = µ

since

they all have zero wealth. Given the linearity of the budget constraint, it follows that newly born

agents’ savings decisions a

s+1

(i) are also normally distributed with mean 0 and variance σ

(s + 1, s) =





[1 − (1 + γρw

) µ

]

. By induction, it follows that for any cohort born at date s, the cross-

sectional distribution of consumption at any date t > s is normal with mean y

and variance

(t, s) = µ

(t, s) + µ

(59)

while the distribution of asset holdings is normal with mean 0 and variance

(t, s) =

t−1

[1 − (1 + γρw

t−1

) µ

t−1

]



(t − 1, s) + w

t−1



(60)

B.2 Objective function of planner

Substituting labor supply (10) into the objective function, we can write the date 0 expected utility of

individual i from the cohort born at date s going forwards as:

(i) = −

∞

t=0

(βϑ)

(1 + γρw

) e

−γc

(i)

= −

∞

t=0

(βϑ)

(1 + γρw

) e

−γy

−γµ

(i)

where we have used labor supply (10), consumption function (9) and the fact that in equilibrium C

= y

We assume that the planner puts a weight of 1 on every individual alive at date 0 and (βϑ)

on individuals’

lifetime welfare who will be born at date t > 0. Then the social welfare function can be written as:

= (1 − ϑ)

s=−∞

−s

(i)di

| {z }

welfare of those alive at date 0

∞

s=1

(1 − ϑ)β

(i)di

| {z }

welfare of the unborn at date 0

Using the deﬁnition of W

(i) and W

(i), notice that W

can be written as:

= −

∞

t=0

(1 + γρw

) e

−γy

where Σ

is deﬁned as:

= (1 − ϑ)

s=−∞

t−s

−γµ

(i)

di (61)

Thus, we can write W

as:

∞

t=0

where U

= −

(1 + γρw

−γy

B.2.1 Derivation of Σ

recursion

Write (61) as:

= (1 − ϑ)

−γµ

(i)

di + (1 − ϑ)

t−1

s=−∞

t−s

−γµ

(i)

= (1 − ϑ) e

+ (1 − ϑ)

t−1

s=−∞

t−s

−γµ

{

(i)+w

(

(i)−ξ

)}

= (1 − ϑ) e

+ (1 − ϑ)

t−1

s=−∞

t−s

−γµ

(i)

−γµ

(

(i)−ξ

)

= e

(1 − ϑ) + (1 −ϑ) ϑ

t−1

s=−∞

t−1−s

−γµ

t−1

[

−1

t−1

−(1+γρw

t−1

)

]

t−1

(i)

where we have used the fact that a

(i) =

t−1

[1 − (1 + γρw

t−1

) µ

t−1

] x

t−1

(i). Also, at all dates t > 0,

we know that µ

−1

t−1

− (1 + γρw

t−1

) =

t−1

−1

. Using this, we have for all t > 0:

ln Σ

+ ln (1 − ϑ + ϑΣ

t−1

) (62)

which is the same as (22) in the main text. Next, imposing steady state up till date 0, we know that

−1

− (1 + γρw) =

β (µ

)

−1

where µ

denotes the date −1 expectation of µ

. Then we can write Σ

as:

= e

(1 − ϑ) + (1 −ϑ) ϑ

−1

s=−∞

−1−s

−γ





µx

−1

(i)

(63)

and the variance of consumption for cohorts born at date s < 0 is γ

(−1, s) = −sΛ. Therefore:

= e







1 − ϑ

1 − ϑe











We also know that in steady state (Σ

−1

= Σ) , [1 − ϑ + ϑΣ

−1

]



1 − ϑe



= (1 −ϑ). Plugging this in the

previous expression yields (23) in the main text:

ln Σ

+ ln [1 − ϑ + ϑΣ

−1

] + ln







1 − ϑe











C Some auxiliary results

In the proofs that follow, we shall make liberal use of the following assumptions and results.

Assumption 1. Throughout the paper, we shall assume that:

1. ϑ ≥

2. βϑ > e

−

= 0.61

3. σ

< σ =

2ρ

ln ϑ

−1



γρ

1+γρ



(

1−

)

ln ϑ

−1

1+2 ln ϑ

+(1−β)

Lemma 2. Given that βϑ > e

−

, we have Λ < 1 and

β < 1.

Proof. Recall that in steady state, Λ = γ

> 0, i.e.:

Λ =



γρw

1 + γρw





1 − βθe



Rearranging:

f (Λ) ≡



1 − βθe





γρw

1 + γρw



(64)

Now, f (Λ) is increasing for Λ < Λ

∗

≡ −2 ln βϑ < 1 given our assumption, and goes to ∞ as Λ → Λ

∗

. For

any values of σ and ρ, we can ﬁnd some 0 < Λ < Λ

∗

satisfying f





. Thus, any solution to (64)

must satisfy Λ ≤ Λ < Λ

∗

< 1. By construction, for any Λ < Λ

∗

β = βθe

< 1.

Lemma 3. For σ < [0, σ), we have ϑe

< 1.

Proof. First we show that ϑe

= 1 implies that σ = σ. Starting from the expressions for wages in steady

state, using ϑe

= 1 we have:

w − 1

1 + γρw

Θ − 1 + Λ

(1 − Λ)(1 −

β)



1 −



ln ϑ

−1

(1 + 2 ln ϑ) (1 − β)

Add 1 to both sides and multiply by

γρ

1+γρ

to get:

γρw

1 + γρw





2 ln ϑ

−1



1 −



(1 + 2 ln ϑ)



1 −



+ 1





γρ

1 + γρ

Next, using the expression above in the deﬁnition of Λ, we have:

2 ln ϑ

−1



γρ

1+γρ



−2 ln ϑ



1−



(1+2 ln ϑ)

+ (1 − β)

which is the same as σ deﬁned in Assumption 1. Second, note that when σ

= 0, we have Λ = 0 and

ϑe

= ϑ < 1. By continuity it follows that for σ ∈ [0, σ), we have ϑe

< 1.

Corollary 1. The following is true:

1 − β

−1

β (1 − Λ) > 0

Proof.

1 − β

−1

β (1 − Λ) = 1 −ϑe

(1 − Λ) > 0

D First-order condition of the planning problem

The planning problem can be written as:

max

∞

t=0



−

(1 + γρw

) e

−γy



s.t.

γy

= γy

t+1

− ln βθ + ln µ

t+1

+ ln



−1

− (1 + γρw

)



−

t+1

2φ(y

t+1

−y)

(Π

− 1) Π

Φ (λ − 1)



1 −

(1 − τ) λw



+ ζ

−1

(Π

t+1

− 1) Π

t+1

ln Σ

2φ(y

−y)

+ ln [1 − ϑ + ϑΣ

t−1

] + I(t = 0) ln







1 − ϑe











= z

ρ ln w

+ ξ

1 + γρz

+ ∆

where ζ



−1

− (1 + γρw

)



t+1



t+1



The problem can be written as a Lagrangian:

L =

∞

t=0



−

(1 + γρw

) e

−γy



∞

t=0

1,t

(

γy

t+1

− ln βθ + ln µ

t+1

+ ln



−1

− (1 + γρw

)



−

t+1

2φ(y

t+1

−y)

− γy

)

∞

t=0

2,t



Φ (λ − 1)



1 −

(1 − τ) λw



+ ζ

(Π

t+1

− 1) Π

t+1

− (Π

− 1) Π



3,0











+ ln [1 − ϑ + ϑΣ

−1

] + ln







1 − ϑe











− ln Σ











∞

t=1

3,t

(

2φ(y

−y)

+ ln [1 − ϑ + ϑΣ

t−1

] − ln Σ

)

∞

t=0

4,t



− z

ρ ln w

+ ξ

1 + γρz

+ ∆



The optimal decisions satisfy:

FOC wrt w

γρw

1 + γρw

+ β

−1

2,t−1

dζ

t−1

(Π

− 1) Π

− M

1,t

γρw

−1

− (1 + γρw

)

2,t



Φ (λ − 1)

(1 − τ) λw

+ w

dζ

(Π

t+1

− 1) Π

t+1



− M

4,t

ρz

1 + γρz

+ ∆

= 0 (65)

FOC y

−γU

− γM

1,t

+ β

−1

2,t−1

dζ

t−1

(Π

− 1) Π

+ M

2,t

dζ

(Π

t+1

− 1) Π

t+1

+β

−1

1,t−1

γ − φγ

t+1

2φ(y

−y)

+ M

3,t

φγ

2φ(y

−y)

+ M

4,t

= 0 (66)

FOC µ

−M

1,t

−1

− 1 − γρw

+ β

−1

1,t−1

1 − γ

2φ(y

−y)

+ β

−1

2,t−1

dζ

t−1

dµ

(Π

− 1) Π

2,t

dζ

dµ

(Π

t+1

− 1) Π

t+1

+ M

3,t

2φ(y

−y)

+ I(t = 0)M

3,0

ϑe





1 − ϑe









= 0

(67)

FOC Σ

− M

3,t

+ βM

3,t+1

ϑΣ

1 − ϑ + ϑΣ

= 0 (68)

FOC Π

−1

2,t−1

t−1

(2Π

− 1) − M

2,t

(2Π

− 1) + M

4,t

ρ ln w

+ ξ

[1 + γρz

+ ∆

]

Ψ (Π

− 1) = 0 (69)

D.1 Steady state of the optimal plan

Next, we impose steady state and set Π = 1. This yields the τ and the multipliers that are consistent with

Π = 1 being optimal in the long-run. Using Π = 1 in (69):



−1

β − 1



= 0

which implies that M

= 0 in steady state. Next, from (68) we have m

= (1 −

β)

−1

where m

= M

/U for

i = {1, 2, 3, 4}. Then equations (65),(66),(67) can be manipulated to yield:

1 −

1 − β

−1

β (1 − Λ)

(70)

w − 1

1 + γρw

= Ω (71)

= γ



1 − β

−1



(1 − Λ)

1 − β

−1

β (1 − Λ)

(1 + Ω) (72)

where Ω =

Θ−(1−Λ)

(1−Λ)

(

1−

)

and Θ = 1−

Λφ

. Finally, using (71) and since Π = 1 in (25) implies that

(1−τ)λw

= 1,

we can write:

w =

1 + Ω

1 − γρΩ

and τ =

λ − 1

1 + γρ

Ω

Ω + 1

which are the same expressions in (27) in the main text.

E Linearized ﬁrst order conditions

Linearizing the ﬁrst-order conditions from the planners problem yields the following:

FOC w

−γ (1 + Ω) by

+ (1 + Ω)

−

1 −

(1 + Ω) bm

1,t

−

1 −



γρ

1 + γρ



(1 + Ω)

−

1 −

(1 + Ω) m

bµ

+ κ

1 + γρ

γρ

2,t

−

4,t

−

1 + γρ

= 0

(73)

FOC y

−

γρ (1 + Ω)

1 + γρ

+ γ

1 + 2

(1 − Θ)



−



−

− bm

1,t

1,t−1

+2 (1 − Θ)



−



bµ

+ (1 − Θ) bm

3,t

4,t

= 0 (74)

FOC π

− bm

2,t

βR

2,t−1

1 + γρ

Φm

= 0 (75)

FOC µ (for dates t ≥ 1)

−

1 −

γρ (1 + Ω)

1 + γρ

2Λ



−



−

1 −

bµ

+ Λ bm

3,t

+2γ (1 − Θ)



−



−

1,t

−

(1 − Λ) bm

1,t−1

= 0 (76)

For t = 0

−

1 −

(1 + Ω)

γρ

1 + γρ

2Λ



−



−

1 −

bµ

+2γ (1 − Θ)



−



ϑΛΣ

1 − ϑ

+ bm

3,0

)

+Λ bm

3,0

+ m



2 +

Λ (1 − ϑ + ϑΣ)

1 − ϑ



ϑΛΣ

1 − ϑ

bµ

−

1,0

−

(1 − Λ) bm

1,−1

= 0 (77)

FOC Σ

γρw

1 + γρw

− γby

− bm

3,t

β bm

3,t+1

1 − β

−1

1 −

= 0 (78)

where bm

for i ∈ {1, 2, 3, 4}.

E.1 Deriving the target criterion

Combine the FOC for bw

(73) and for by

(74):

γΩby

+ 2γ

(1 − Θ)



−



+ Ω

−





1 +

1 −

(1 + Ω) m





γρ (1 + Ω)

1 + γρ

2 (1 − Θ)



−



−

1 −

(1 + Ω) m

bµ

+ κ

1 + γρ

γρ

2,t

+ (1 − Θ) bm

3,t

−

1 + γρ

−

1 + Ω



1 −



1,t

−

(1 − Λ) bm

1,t−1

= 0

(79)

Combine with (76):

Ω + 2γ

(1 − Θ)



−



− 2

1 + Ω



1 −

i

(1 − Θ)



−



+ Ω







1 + Ω



1 −

i

1 −

γρ (1 + Ω)

1 + γρ

−





1 +

1 −

(1 + Ω) m





γρ (1 + Ω)

1 + γρ







2 (1 − Θ)



−



−

1 −

(1 + Ω) m

bµ

−

1 + Ω



1 −

i

2Λ



−



−

1 −

bµ



1 − Θ − Λ

1 + Ω



1 −

i

3,t

+ κ

1 + γρ

γρ

2,t

−

1 + γρ

= 0

Next, use the GDP deﬁnition (21) to substitute out for

Ω + 2γ

(1 − Θ)



−



− 2

1 + Ω



1 −

i

(1 − Θ)



−



+ Ω







1 + Ω



1 −

i

1 −

γρ (1 + Ω)

1 + γρ

−





1 +

1 −

(1 + Ω) m





γρ (1 + Ω)

1 + γρ







1 + γρ

−







1 + Ω



1 −

i

1 −

γρ (1 + Ω)

1 + γρ

−





1 +

1 −

(1 + Ω) m





γρ (1 + Ω)

1 + γρ







2 (1 − Θ)



−



−

1 −

(1 + Ω) m

bµ

−

1 + Ω



1 −

i

2Λ



−



−

1 −

bµ



1 − Θ − Λ

1 + Ω



1 −

i

3,t

+ κ

1 + γρ

γρ

2,t

−

1 + γρ

= 0

Substitute out for bµ

using bµ

= Γ

−γ

1 +



1 −



Ω

and using the deﬁnitions of m

, m

and m

, the

above can be written as:

1 − β

−1

β (1 − Λ)

γΩ







1 −



Ω + 1 + 2



1 − β

−1





1 −



Ω





− γΩby



1 − β

−1



(1 − Λ)

1 − β

−1

β (1 − Λ)

(Ω + 1)



−

ρ + y

1 + γρ



− Ω

Λ + 2



1 − β

−1



1 − β

−1

β (1 − Λ)

+κ

1 + γρ

γρ

2,t

+ Ω

−



1 −



Ω bm

3,t

= 0 (80)

Guess that:

3,t

1 −

+ γΩby

+ a

(81)

and use this in (78) with

substituted out using the deﬁnition of GDP:

t+1

− β

−1

+ γ



1 −



Ωby

t+1

1 −



γ (1 + Ω)

1 + γρ

+ a



1 −

β%





using the fact that bz

t+1

= %

. Using the date t + 1 Σ recursion (45):

ΛΓ

t+1

1 −



γ (1 + Ω)

1 + γρ

+ a



1 −

β%





Using the fact that Γ

γy

1+γρ

(

1−

)

(1+Ω)

1−

β%

(1−Λ)

, we have:

Λ%

γy

1 + γρ



1 −



(1 + Ω)

1 −

β%

(1 − Λ)

1 −



γ (1 + Ω)

1 + γρ

+ a



1 −

β%





which implies that a

must satisfy:

= −

γ (1 + Ω)

1 −

βρ

(1 − Λ)

1 + γρ

(82)

Using bm

3,t

1−

+ γΩby

+ a

in (80):

α (Ω)



− δ (Ω) by



= η

for t > 0 (83)

where we have deﬁned η

= −

κ(1+γρ)

2,t

where

α (Ω) = 1 − γρ

Ω

1 + Ω







1 −



Ω + 1 − 2



1 −



Ω

Λ (1 − Λ)





and

δ (Ω) = α (Ω)

−1







1 +



1 −



Ω

1 −

βρ

(1 − Λ)

ρy

ρ + y



1 + Λ

1 − Λ









Similarly, for the date 0 target criterion, combine the date 0 version of (79) with (77), (81) and the date 1

Σ recursion (45) to get:

(Ω)



− δ

(Ω) by

− χ (Ω)



= η

(84)

where

(Ω) = α (Ω) +

1 +



1 −



Ω

1 −



2 + Λ + 2

ΛϑΣ

1 − ϑ



ϑΛΣ

1 − ϑ

(85)

(Ω) = α

(Ω)

−1





α (Ω) δ (Ω) + γ

(Ω + 1)



1 + 2Λ + 2

ΛϑΣ

1 − ϑ



ϑΛΣ

1 − ϑ

1 +



1 −



Ω

1 −

βρ

(1 − Λ)

ρy

y + ρ





(86)

χ (Ω) = α

(Ω)

−1

γρ

1 + (1 −

β)Ω

1 −

ϑΛΣ

1 − ϑ

In summary, using (84)-(83) and the target criterion can be written as:







(Ω)



− δ

(Ω)by

− χ(Ω)



for t = 0

α(Ω)



− δ(Ω)by



for t ≥ 1

This is the same as (46) in the main text. Next, multiplying (75) by

κ(1+γρ)

yields:

βR

t−1

−

λ − 1

yπ

which is the same as equation (47) in the main text. This concludes the derivation of the expressions in

Proposition 4.

E.1.1 Derivation of expressions in Proposition 3

Deﬁne the scalars α = α

(0) and δ = δ

(0) and χ = χ(0):

α ≡ α

(0) = 1 +

1 −



2 + Λ + 2

ΛϑΣ

1 − ϑ



ϑΛΣ

1 − ϑ

> 1

δ ≡ δ

(0) = α

−1

1 +

1 −



1 + 2Λ + 2

ΛϑΣ

1 − ϑ



ϑΛΣ

1 − ϑ

1 −

βρ

(1 − Λ)

1 + ρ

χ = χ (0) = α

−1

γρ

ϑΛΣ

1 − ϑ

> 0

Since

1−

βρ

(1−Λ)

1+ρ

< 1, it is clear that δ < 1. It is also clear by inspection that α(0) = δ(0) = 1. Thus,

the optimal target criterion when Ω = 0 can be written as:









− δby

− χ



for t = 0

− by

for t ≥ 1

which is the same as equation (38). Finally, when Ω = 0, y = 1 and so (47) becomes (39).

E.1.2 Optimal target criterion in RANK

Recall that in RANK we have Ω = 0 and Λ = 0. In this case, it is clear from inspection that the coeﬃcients

further simplify to α = δ = 1, χ = 0 and the target criterion can be written as:

= by

− by

for t ≥ 0

which is the same as (29) in the main text

E.2 Properties of coeﬃcients α

(Ω), δ

(Ω), α(Ω), δ(Ω)

Claim: α(Ω) > 1

Proof.

α(Ω) = 1 +

ργΩ

1 + Ω



Λ (1 − Λ)

− 1





1 −



Ω − 1



> 1 +

ργΩ

1 + Ω







Λ (1 − Λ)

− 1





1 −





1 −



(1 − Λ)

− 1





where we have used the fact that Ω =

Θ−1+Λ

(1−

β)(1−Λ)

and for countercycical risk (Θ > 1), we have Ω >

(1−

β)(1−Λ)

. Then, the above can be simpliﬁed to:

α(Ω) > 1 +

ργΩ

1 + Ω

1 + Λ

(1 − Λ)

> 1

Claim: If risk is countercyclical Θ > 1, then δ(Ω) < 1

Proof. Countercyclical risk or Θ > 1 implies that Ω >

(1−

β)(1−Λ)

Proof. Notice that δ(Ω) can be written as:

δ(Ω) =

1 + Ω + (Ω + Ω

)

(

1−

)

1−

βρ

(1−Λ)

ρy

ρ+y

1+Λ

1−Λ

1 + (1 − ργ)Ω + ργΩ



Λ(1−Λ)

− 1



1 −



We need to show that δ(Ω) < 1, i.e.

1 + Ω + (Ω + Ω

)



1 −



1 −

βρ

(1 − Λ)

ρy

ρ + y



1 + Λ

1 − Λ



< 1 + (1 − ργ)Ω + ργΩ



Λ (1 − Λ)

− 1





1 −



This expression can be simpliﬁed to yield:

1 +



1 −



1 −

βρ

(1 − Λ)

ρ + y



1 + Λ

1 − Λ



< Ω



1 −





Λ (1 − Λ)

− 1



−

1 −

βρ

(1 − Λ)

ρ + y



1 + Λ

1 − Λ



(87)

First, we show that the term in the square brackets on the RHS of (87) is positive, i.e.

2 > Λ

1 − Λ +

1 + Λ

1 −

βρ

(1 − Λ)

ρ + y

The worst case for this to be true is if y is very large and %

= 1. In that case, for the expression above to

be true, it must be that:

β <

2 − (1 − Λ) Λ

which is true since

β < 1 and

2−(1−Λ)Λ

> 1 since we know that 0 < Λ < 1 from Appendix XXX. Thus, the

term in the square brackets on the RHS of (87) is positive.

Next, to show that (87) holds with countercyclical risk, it suﬃces to show that it holds for the lowest

Ω consistent with non-procyclical risk, i.e. Ω =

(1−

β)(1−Λ)

. Plug in Ω =

(1−

β)(1−Λ)

into (87), i.e:

1 +



1 −



(1 + Λ)

1 −

βρ

(1 − Λ)

ρ + y



Λ (1 − Λ)

− 1



−

1 + Λ

1 −

βρ

(1 − Λ)

ρ + y



1 − Λ



Again the worst case for this condition to be satisﬁed is if %

= 1. Suppose that is the case. Then, the

expression can be further simpliﬁed to:

ρ + y

< 1

which is true since steady state output is positive.

Claim: If risk is countercyclical Θ > 1, then α

(Ω) > 1

Proof. Since α(Ω) > 1, it follows from (85) that α

(Ω) > 1.

F The model with nominal debt

In this extension, we change the assumption that ﬁnancial intermediaries trade real claims with the house-

holds. Instead, we assume that now these intermediaries trade nominal claims at a nominal price

1+i

which pay a dollar tomorrow. Then the household’s budget constraint can be written as:

(i) +

1 + i

t+1

(i) = P

(i) + A

(i) + P

where A

t+1

(i) is the quantity of nominal claims purchased by the household at date t. Dividing through

by P

, we get:

(i) +

1 + i

t+1

(i) = w

(i) + a

(i) + T

where a

(i) =

(i)

denotes the real value of wealth held by the household at the beginning of date t.

Given these deﬁnitions, the rest of the model is the same except for the µ

recursion which can now be

written as:

−1

= 1 + γρw

ϑΠ

t+1

1 + i

−1

t+1

the Σ

recursion which we now derive. We start with the budget constraint of a households and plug in

the expression for labor supply (10) and the consumption function (9):

(i) =

1 + i

t−1

ϑΠ



t−1

(i) + a

t−1

(i) + T

t−1

− c

t−1

(i)



t−1

[1 − (1 + γρw

t−1

) µ

t−1

] x

t−1

(i)

In steady state, (12) implies that

[1 − (1 + γρw) µ] = 1, so we can write:

(i) =

[1 − (1 + γρw) µ] x

t−1

(i) = x

t−1

(i)

If we were in steady state up till date 0, the distribution of assets which would obtain at date 0 if there

was no inﬂation between t = −1 and t = 0:

˜a

(i) = w

−1

k=s



(i) − ξ



and

(s, 0) = σ

(−s)

But if there is inﬂation, then actual a

(i) is:

(i) = w

−1

k=s



(i) − ξ



−1

This implies that for cohort born at date s < 0, a

(i) is normally distributed with mean 0 and variance

−sw

−2

. Next, we use this information to derive the expression for Σ

. Using the same Pareto weights

as in the baseline model, we have from (63):

= (1 − ϑ)

s=−∞

−s

−γµ

(i)

= (1 − ϑ)

s=−∞

−s

−γµ

(i)

−γµ

(

−ξ

)

= (1 − ϑ) e

s=−∞

−s

−



µΠ



= (1 − ϑ)

1 − ϑe



µΠ



where on the last line we have used the fact that for cohorts born at dates s < 0, a

(i) ∼ N



0, −sw

−2



This expression can be manipulated to yield:

ln Σ

+ ln [1 − ϑ + ϑΣ] + ln





1 − ϑe



−1







| {z }

eﬀect of date 0 surprise

Of course, for dates t > 0, the Σ recursion stays the same as in the baseline model since the planner is

not able to create any inﬂation surprise at dates t ≥ 1. In linearized terms, the Σ recursion can be written

as:











−γ



1 −



Ωby

+ ΛΓ

βR

t−1

for t > 0

−γ



1 −



Ωby

+ ΛΓ

ϑΛΣ

1−ϑ

(bµ

− π

) for t = 0

F.1 Optimal monetary policy

The monetary policy problem is very similar to the baseline case. The only diﬀerence is the expression for

since now the planner can aﬀect the level of consumption inequality by creating an inﬂation surprise

at date 0. In linearized form, the only ﬁrst order conditions that diﬀer from those in Section E is the date

0 ﬁrst-order condition with respect to inﬂation and with respect to µ. In linearized form, the ﬁrst order

conditions for π can now be written as:

For t = 0

− bm

2,0



1 + γρ

Ψm

+ m

ϑΛΣ

1 − ϑ



−

ΛϑΣ

1 − ϑ

3,0

−m

ϑΛΣ

1 − ϑ



2 + Λ +

ϑΛΣ

1 − ϑ



(bµ

− π

) −m

ϑΛΣ

1 − ϑ

= 0

(88)

and for t ≥ 1

− bm

2,t

βR

2,t−1

1 + γρ

Ψm

= 0 (89)

and the FOCs for µ can be written as:

For t = 0

−

1 −

(1 + Ω)

γρ

1 + γρ

2Λ



−



−

1 −

bµ

+2γ (1 − Θ)



−



ϑΛΣ

1 − ϑ

+ bm

3,0

) (90)

+Λ bm

3,0

+ m



2 +

Λ (1 − ϑ + ϑΣ)

1 − ϑ



ϑΛΣ

1 − ϑ

(bµ

− π

) −

1,0

−

(1 − Λ) bm

1,−1

= 0

and for t ≥ 1

−

1 −

(1 + Ω)

γρ

1 + γρ

2Λ



−



−

1 −

bµ

(91)

+2γ (1 − Θ)



−



+ Λ bm

3,0

−

1,t

−

(1 − Λ) bm

1,t−1

= 0

F.2 Deriving the target criterion

It is clear that the target criterion for dates t ≥ 1 is unchanged. The only diﬀerence is in the date 0 target

criterion, which we derive next. In this case with nominal debt, the date 0 version of the combined FOC

for w and y (79) can be written as:

γΩby

+ 2γ

(1 − Θ)



−



+ Ω

−





1 +

1 −

(1 + Ω) m





γρ (1 + Ω)

1 + γρ

2 (1 − Θ)



−



−

1 −

(1 + Ω) m

bµ

+ κ

1 + γρ

γρ

2,0

+ (1 − Θ) bm

3,0

−

1 + γρ

−

1 + Ω



1 −



1,0

−

(1 − Λ) bm

1,−1

= 0

Multiply (90) by −

1 + Ω



1 −

i

and add to the equation above to get:







1 − β

−1

β (1 − Λ)

γΩ







1 −



Ω + 1 + 2



1 − β

−1





1 −



Ω





− γΩ +

ργ







−

ργ

ρ + y

1 + γρ

− Ω

Λ + 2



1 − β

−1



1 − β

−1

β (1 − Λ)

+ κ

1 + γρ

γρ

2,0

+ Ω

−



1 −



Ω bm

3,0

−

1 +



1 −



Ω

ϑΛΣ

1 − ϑ

3,0

−





1 +



1 −



Ω

1 −





ϑΛΣ

1 − ϑ

−





1 +



1 −



Ω

1 −







2 +

Λ (1 − ϑ + ϑΣ)

1 − ϑ



ϑΛΣ

1 − ϑ

+γ

1 +



1 −



Ω

1 −



2 +

Λ (1 − ϑ + ϑΣ)

1 − ϑ



ϑΛΣ

1 − ϑ





1 + Ω



1 −



1 −







2 +

Λ (1 − ϑ + ϑΣ)

1 − ϑ



ϑΛΣ

1 − ϑ

= 0

Guess

3,0

1 −

+ γΩby

−

γ (1 + Ω)

1 −

βρ

(1 − Λ)

1 + γρ

Plug this into the expression above:







1 − β

−1

β (1 − Λ)

γΩ







1 −



Ω + 1 + 2



1 − β

−1





1 −



Ω





ργ

− γΩ

1 +



1 −



Ω







−m







1 −



Ω

1 −

βρ

(1 − Λ)

y + ρ



1 + Λ

1 − Λ



ργ





+ κ

1 + γρ

γρ

2,0

+γ

1 +



1 −



Ω

ϑΛΣ

1 − ϑ







2Ω +





1 +



1 −



Ω

1 −









1 +

ϑΛΣ

1 − ϑ



+ Λ









−





1 +



1 −



Ω

1 −

βρ

(1 − Λ)





ϑΛΣ

1 − ϑ

γ (1 + Ω)

y + ρ



1 + 2



Λ +

ϑΛΣ

1 − ϑ







1 + Ω



1 −



1 −





ϑΛΣ

1 − ϑ





1 +

ϑΛΣ

1 − ϑ



+ Λ



−





1 +



1 −



Ω

1 −





ϑΛΣ

1 − ϑ

= 0

This expression can be rearranged to yield:

(Ω) [by

− δ

(Ω) by

+ ι (Ω) π

− χ (Ω)] = η

where

(Ω) ι (Ω) =

γρ





1 + Ω



1 −



1 −





ϑΛΣ

1 − ϑ





1 +

ϑΛΣ

1 − ϑ



+ Λ



and α

(Ω) , δ

(Ω) and χ (Ω) are as deﬁned in Appendix E.1.

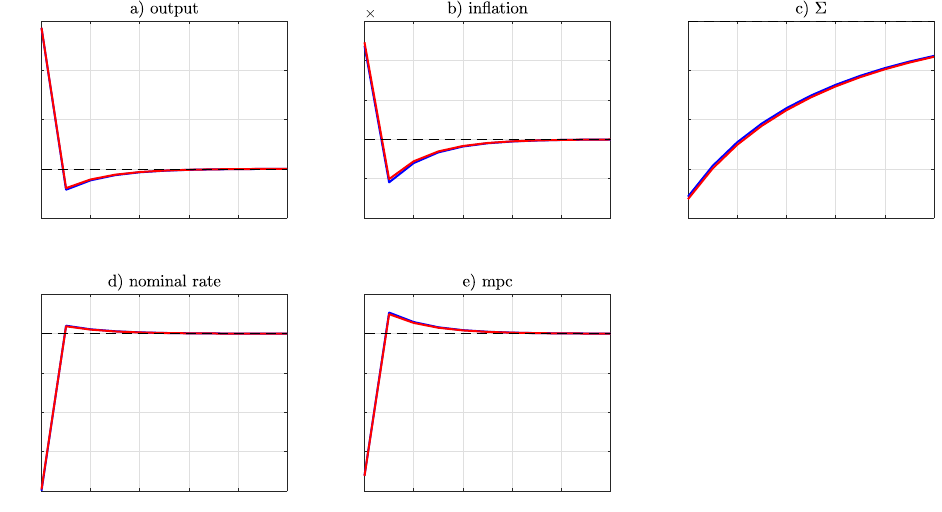
0 2 4 6 8 10

-0.02

0.02

0.04

0.06

0 2 4 6 8 10

-2

-1

-3

0 2 4 6 8 10

-0.04

-0.03

-0.02

-0.01

0 2 4 6 8 10

-0.2

-0.15

-0.1

-0.05

0.05

0 2 4 6 8 10

-0.2

-0.15

-0.1

-0.05

0.05

Figure 8. Time inconsistency with nominal debt: Optimal dynamics absent shocks in baseline calibration (κ = 0.01).

Blue line denotes HANK with countercylcical risk and real debt, red line denotes HANK with countercyclical risk and nominal

debt. All variables are plotted as percentage deviations from their steady state values.